题目内容
【题目】设函数![]() 的图象为
的图象为![]() ,
, ![]() 关于点
关于点![]() 对称的图象为
对称的图象为![]() ,
, ![]() 对应的函数为
对应的函数为![]() .
.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)若直线![]() 与
与![]() 只有一个交点,求
只有一个交点,求![]() 的值和交点坐标.
的值和交点坐标.
【答案】(1)![]() (2)当m=0时,,交点为(3,0);当m=4时,,交点为(5,4).
(2)当m=0时,,交点为(3,0);当m=4时,,交点为(5,4).
【解析】试题分析:(1)设点P(x,y) 关于点A(2,1)对称的点为P′,代入解析式f(x)=x+![]() ,可得
,可得![]() 的解析式;(2)即
的解析式;(2)即![]() 与
与![]() 组成方程组只有一解,由判别式为零可得
组成方程组只有一解,由判别式为零可得![]() 的值,代入方程可得交点坐标.
的值,代入方程可得交点坐标.
试题解析:解:(Ⅰ)设点P(x,y)是C2上的任意一点,
则P(x,y)关于点A(2,1)对称的点为P′(4![]() -x,2-y),
-x,2-y),
代入f(x)=x+![]() ,可得2-y=4-x+
,可得2-y=4-x+![]() ,即y=x-2+
,即y=x-2+![]() ,
,
∴g(x)=x-2+![]() .
.
(Ⅱ)由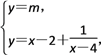 消去y
消去y
得x2-(m+6)x+4m+9=0,Δ=(m+6)2-4(4m+9),
∵直线y=m与C2只有一个交点,∴Δ=0,解得m=0或m=4.
当m=0时,经检验合理,交点为(3,0);
当m=4时,经检验合理,交点为(5,4).

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目