题目内容
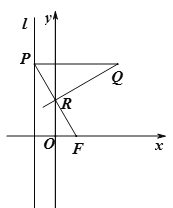
【题目】设点
，直线
，点
在直线
上移动， 
是线段
与
轴的交点, 
.
(Ⅰ) 求动点
的轨迹
的方程；
（Ⅱ）直线
与
轴相交于点
,过
的直线
交轨迹
于
两点，
试探究点
与以
为直径的圆的位置关系,并加以说明．
【答案】（1）
（2）点
在以
为直径的圆上或外
【解析】试题分析：（1）由垂直平分线性质将条件转化为
．再根据抛物线定义可得动点
的轨迹
是以
为焦点， 
为准线的抛物线，最后根据性质求抛物线标准方程（2）直径AB中点即圆心到直线
的距离等于A、B两点到直线
的距离和的一半，而由抛物线定义有A、B两点到直线
的距离和为
,因此以
为直径的圆与直线
相切，进而可判断点
与以
为直径的圆的位置关系
试题解析：解：(Ⅰ)依题意知： 
是线段
的垂直平分线．∴
是点
到直线
的距离．∵点
在线段
的垂直平分线，∴
．
故动点
的轨迹
是以
为焦点， 
为准线的抛物线， 其方程为： 
．
（Ⅱ）法一：设A、B两点到直线
的距离分别为
，
直径AB中点N到直线
的距离分别为
，
由抛物线定义知
, ∴
∴以
为直径的圆与直线
相切
法二：
（1）当AB垂直
轴时，以
为直径的圆
点
为切点，
∴点
与以
为直径的圆上
（2）当直线
与
轴不垂直时， 
∴点
与以
为直径的圆外
①当直线AB垂直于
轴时，易知以
为直径的圆方程为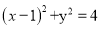
，
点
满足方程，∴点
与以
为直径的圆上
②当直线
与
轴不垂直时，
设直线AB方程为
与抛物线交点
， 
，
联立
，
显然
且
， 圆直径
AB中点N的坐标（
，
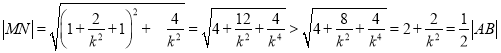，∴点
与以
为直径的圆外
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
【题目】某服装销售公司进行关于消费档次的调查，根据每人月均服装消费额将消费档次分为0-500元；500-1000元；1000-1500元；1500-2000元四个档次，针对
两类人群各抽取100人的样本进行统计分析，各档次人数统计结果如下表所示：
| 0～ 500元 | 500～ 1000元 | 1000～ 1500元 | 1500～ 2000元 |
A类 | 20 | 50 | 20 | 10 |
B类 | 50 | 30 | 10 | 10 |
月均服装消费额不超过1000元的人群视为中低消费人群，超过1000元的视为中高收入人群.
（Ⅰ）从
类样本中任选一人，求此人属于中低消费人群的概率；
（Ⅱ）从两类人群中各任选一人，分别记为甲、乙，估计甲的消费档次不低于乙的消费档次的概率；
（Ⅲ）以各消费档次的区间中点对应的数值为该档次的人均消费额，估计两类人群哪类月均服装消费额的方差较大（直接写出结果，不必说明理由）.
