题目内容
【题目】设函数![]() ,
, ![]() =
= ![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若函数![]() 有两个零点
有两个零点![]() .
.
(1)求满足条件的最小正整数![]() 的值;
的值;
(2)求证: ![]() .
.
【答案】(Ⅰ)![]() 的单调增区间为
的单调增区间为 ,单调减区间为
,单调减区间为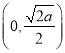 ;
;
(Ⅱ)(1)3;(2)见解析.
【解析】试题分析:
(Ⅰ)求单调区间,只要求得导数![]() ,通过讨论
,通过讨论![]() 的范围(
的范围(![]() 和
和![]() )可解不等式
)可解不等式![]() 和不等式
和不等式![]() ,从而得单调区间;
,从而得单调区间;
(Ⅱ)(1)求得![]() ,由
,由![]() 有两个零点得
有两个零点得![]() ,
, ![]() 的最小值为
的最小值为![]() ,且
,且![]() , 由此可得
, 由此可得![]() ,由函数
,由函数![]() 是增函数,通过估值可得最小正整数
是增函数,通过估值可得最小正整数![]() 的值;(2)证明
的值;(2)证明![]() ,设
,设![]() ,由
,由![]() ,可把
,可把![]() 用
用![]() 表示,不等式
表示,不等式![]() 中的
中的![]() 可替换,然后变形为
可替换,然后变形为![]() 的不等式,设
的不等式,设![]() ,则
,则![]() ,只要证相应地关于
,只要证相应地关于![]() 的不等式在
的不等式在![]() 上成立,这又可用导数研究相应的函数得出.
上成立,这又可用导数研究相应的函数得出.
试题解析:
(Ⅰ)![]() .
.
当![]() 时,
时, ![]() 在
在![]() 上恒成立,所以函数
上恒成立,所以函数![]() 单调递增区间为
单调递增区间为![]() ,
,
此时![]() 无单调减区间.
无单调减区间.
当![]() 时,由
时,由![]() ,得
,得![]() ,
, ![]() ,得
,得![]() ,
,
所以函数![]() 的单调增区间为
的单调增区间为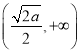 ,单调减区间为
,单调减区间为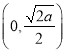 .
.
(Ⅱ)(1)![]() .
.
因为函数![]() 有两个零点,所以
有两个零点,所以![]() ,此时函数
,此时函数![]() 在
在![]() 单调递增, 在
单调递增, 在![]() 单调递减.
单调递减.
所以![]() 的最小值
的最小值![]() ,即
,即![]() .
.
因为![]() ,所以
,所以![]() .
.
令![]() ,显然
,显然![]() 在
在![]() 上为增函数,且
上为增函数,且
![]() ,所以存在
,所以存在![]() .
.
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,所以满足条件的最小正整数
,所以满足条件的最小正整数![]() .
.
又当![]() 时,
时, ![]() ,所以
,所以![]() 时,
时, ![]() 有两个零点.
有两个零点.
综上所述,满足条件的最小正整数![]() 的值为3.
的值为3.
(2)证明 :不妨设![]() ,于是
,于是![]()
即![]() ,
,
![]() .
.
所以![]() .
.
因为![]() ,当
,当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
故只要证![]() >
>![]() 即可,即证明
即可,即证明![]() ,
,
即证![]() ,
,
也就是证![]() .
.
设![]() .
.
令![]() ,则
,则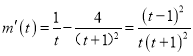 .
.
因为![]() ,所以
,所以![]() ,
,
当且仅当![]() 时,
时, ![]() ,
,
所以![]() 在
在![]() 上是增函数.
上是增函数.
又![]() ,所以当
,所以当![]() 总成立,所以原题得证.
总成立,所以原题得证.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目