题目内容
如图,圆锥顶点为P,底面圆心为O,其母线与底面所成的角为22.5°,AB和CD是底面圆O上的两条平行的弦,轴OP与平面PCD所成的角为60°,
(1)证明:平面PAB与平面PCD的交线平行于底面;
(2)求cos∠COD.

(1)证明:平面PAB与平面PCD的交线平行于底面;
(2)求cos∠COD.

(1)证明:设平面PAB与平面PCD的交线为l,则
∵AB∥CD,AB?平面PCD,∴AB∥平面PCD
∵AB?面PAB,平面PAB与平面PCD的交线为l,∴AB∥l
∵AB在底面上,l在底面外
∴l与底面平行;
(2)设CD的中点为F,连接OF,PF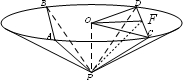
由圆的性质,∠COD=2∠COF,OF⊥CD
∵OP⊥底面,CD?底面,∴OP⊥CD
∵OP∩OF=O
∴CD⊥平面OPF
∵CD?平面PCD
∴平面OPF⊥平面PCD
∴直线OP在平面PCD上的射影为直线PF
∴∠OPF为OP与平面PCD所成的角
由题设,∠OPF=60°
设OP=h,则OF=OPtan∠OPF=
h
∵∠OCP=22.5°,∴OC=
=
∵tan45°=
=1
∴tan22.5°=
-1
∴OC=
=(
+1)h
在Rt△OCF中,cos∠COF=
=
=
-
∴cos∠COD=cos(2∠COF)=2cos2∠COF-1=17-12
∵AB∥CD,AB?平面PCD,∴AB∥平面PCD
∵AB?面PAB,平面PAB与平面PCD的交线为l,∴AB∥l
∵AB在底面上,l在底面外
∴l与底面平行;
(2)设CD的中点为F,连接OF,PF

由圆的性质,∠COD=2∠COF,OF⊥CD
∵OP⊥底面,CD?底面,∴OP⊥CD
∵OP∩OF=O
∴CD⊥平面OPF
∵CD?平面PCD
∴平面OPF⊥平面PCD
∴直线OP在平面PCD上的射影为直线PF
∴∠OPF为OP与平面PCD所成的角
由题设,∠OPF=60°
设OP=h,则OF=OPtan∠OPF=
| 3 |
∵∠OCP=22.5°,∴OC=
| OP |
| tan∠OCP |
| h |
| tan22.5° |
∵tan45°=
| 2tan22.5° |
| 1-tan222.5° |
∴tan22.5°=
| 2 |
∴OC=
| h | ||
|
| 2 |
在Rt△OCF中,cos∠COF=
| OF |
| OC |
| ||
(
|
| 6 |
| 3 |
∴cos∠COD=cos(2∠COF)=2cos2∠COF-1=17-12
| 2 |

练习册系列答案
相关题目