题目内容
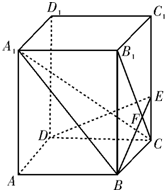
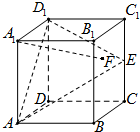
在正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内的动点,且A1F∥平面D1AE,则A1F与平面BCC1B1所成角的正切值构成的集合是( )
A.{t|
| B.{t|
| C.{t|2≤t≤2
| D.{t|2≤t≤2
|

设平面AD1E与直线BC交于点G,连接AG、EG,则G为BC的中点
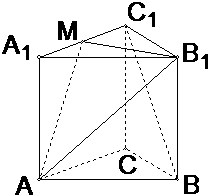
分别取B1B、B1C1的中点M、N,连接AM、MN、AN,则
∵A1M∥D1E,A1M?平面D1AE,D1E?平面D1AE,
∴A1M∥平面D1AE.同理可得MN∥平面D1AE,
∵A1M、MN是平面A1MN内的相交直线
∴平面A1MN∥平面D1AE,
由此结合A1F∥平面D1AE,可得直线A1F?平面A1MN,即点F是线段MN上上的动点.
设直线A1F与平面BCC1B1所成角为θ
运动点F并加以观察,可得
当F与M(或N)重合时,A1F与平面BCC1B1所成角等于∠A1MB1,此时所成角θ达到最小值,满足tanθ=
=2;
当F与MN中点重合时,A1F与平面BCC1B1所成角达到最大值,满足tanθ=
=2
∴A1F与平面BCC1B1所成角的正切取值范围为[2,2
]
故选:D
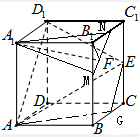
分别取B1B、B1C1的中点M、N,连接AM、MN、AN,则
∵A1M∥D1E,A1M?平面D1AE,D1E?平面D1AE,
∴A1M∥平面D1AE.同理可得MN∥平面D1AE,
∵A1M、MN是平面A1MN内的相交直线
∴平面A1MN∥平面D1AE,
由此结合A1F∥平面D1AE,可得直线A1F?平面A1MN,即点F是线段MN上上的动点.
设直线A1F与平面BCC1B1所成角为θ
运动点F并加以观察,可得
当F与M(或N)重合时,A1F与平面BCC1B1所成角等于∠A1MB1,此时所成角θ达到最小值,满足tanθ=
| A1B1 |
| B1M |
当F与MN中点重合时,A1F与平面BCC1B1所成角达到最大值,满足tanθ=
| A1B1 | ||||
|
| 2 |
∴A1F与平面BCC1B1所成角的正切取值范围为[2,2
| 2 |
故选:D


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目