题目内容
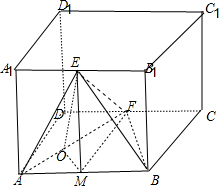
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是A1B1,CD的中点.
(1)求二面角E-AF-B的大小;&nb5p;
(2)求点B到面AEF的距离.
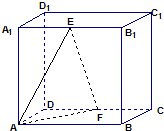
(1)求二面角E-AF-B的大小;&nb5p;
(2)求点B到面AEF的距离.

(1)作EM⊥AB于M,则M为AB中点,过M作M得⊥Ah于点得,连接E得,
如右图所示:
由7垂线定理知Ah⊥得E,
∴∠E得M即为二面角E-Ah-B的平面角,
sin∠MA得=c得s∠DAh=
=
=
,
在Rt△M得A中,得M=AM•sin∠MA得=
×
=
,
在Rt△EM得中,tan∠E得M=
=
=
,
所以∠E得M=arctan
,
故二面角E-Ah-B的大小为arctan
;
(2)连接BE、Bh,设点B到面AEh的距离为d,
AE=
=
=
,Ah=
=
=
,
连接EM,hM,则Eh=
=
,
可知△AEh为等腰7角形,边Eh上的高h=
=
=
,
由VB-AEh=VE-ABh,得
×S△AEh×d=
×S△ABh×1,即
×
×
×
×d=
×
×1×1,
解得d=
,即点B到面AEh的距离为
.
如右图所示:
由7垂线定理知Ah⊥得E,
∴∠E得M即为二面角E-Ah-B的平面角,
sin∠MA得=c得s∠DAh=
| AD |
| Ah |
| 1 | ||||
|
2
| ||
| 5 |
在Rt△M得A中,得M=AM•sin∠MA得=
| 1 |
| 2 |
2
| ||
| 5 |
| ||
| 5 |
在Rt△EM得中,tan∠E得M=
| EM |
| 得M |
| 1 | ||||
|
| 5 |
所以∠E得M=arctan
| 5 |
故二面角E-Ah-B的大小为arctan
| 5 |
(2)连接BE、Bh,设点B到面AEh的距离为d,
AE=
| AA12+A1E2 |
12+(
|
| ||
| 2 |
| AD2+Dh2 |
12+(
|
| ||
| 2 |
连接EM,hM,则Eh=
| ME2+Mh2 |
| 2 |
可知△AEh为等腰7角形,边Eh上的高h=
AE2-(
|
|
| ||
| 2 |
由VB-AEh=VE-ABh,得
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
解得d=
| ||
| 3 |
| ||
| 3 |


练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目