题目内容
正四面体（所有面都是等边三角形的三棱锥）相邻两侧面所成二面角的余弦值是______．
取CD的中点E，连接AE，BE，如下图所示：
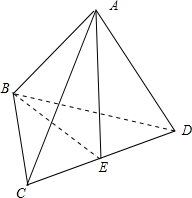
设四面体的棱长为2，则AE=BE=
且AE⊥CD，BE⊥CD，则∠AEB即为相邻两侧面所成二面角的平面角
在△ABE中，cos∠AEB=
=
故正四面体（所有面都是等边三角形的三棱锥）相邻两侧面所成二面角的余弦值是
故答案为：
设四面体的棱长为2，则AE=BE=
| 3 |
且AE⊥CD，BE⊥CD，则∠AEB即为相邻两侧面所成二面角的平面角
在△ABE中，cos∠AEB=
| AE2+BE2-AB2 |
| 2AE•BE |
| 1 |
| 3 |
故正四面体（所有面都是等边三角形的三棱锥）相邻两侧面所成二面角的余弦值是
| 1 |
| 3 |
故答案为：
| 1 |
| 3 |
练习册系列答案
53天天练系列答案
相关题目
