题目内容
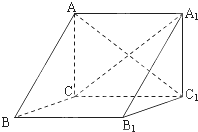
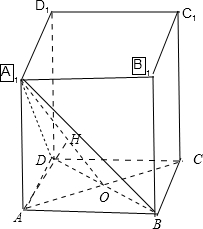
已知正方体ABCD-A1B1C1D1,则直线AB与平面BDA1所成角的正弦值等于______.
设AC∩BD=O,AB=a,
则 BD=
a,A1O=
=
a;
过A作AH⊥平面BDA1于点H,则∠BAH直线AB与平面BDA1所成角;
∵VA1-ABD=VA-A1BD
∴
A1A•S△ABD=
•AH•S△A1BD=
•AH•
×BD×A1O;
即
•a×
×a×a=
•AH•
×
a×
a
∴AH=
a,
在RT△ABH中,cos∠AHB=
=
=
,
∴sin∠AHB=
=
.
即直线AB与平面BDA1所成角的正弦值等于:
.
故答案为:
.
则 BD=
| 2 |
| AO2+A1A2 |
| ||
| 2 |
过A作AH⊥平面BDA1于点H,则∠BAH直线AB与平面BDA1所成角;
∵VA1-ABD=VA-A1BD
∴
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
即
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
∴AH=
| ||
| 3 |
在RT△ABH中,cos∠AHB=
| AH |
| AB |
| ||||
| a |
| ||
| 3 |
∴sin∠AHB=
| 1-cos2∠AHB |
| ||
| 3 |
即直线AB与平面BDA1所成角的正弦值等于:
| ||
| 3 |
故答案为:
| ||
| 3 |


练习册系列答案
相关题目