题目内容
已知定义域为R的函数f(x)为奇函数,且满足f(x+2)=-f(x),当x∈[0,1]时,f(x)=2x-1.
(1)求f(x)在[-1,0)上的解析式;
(2)求f(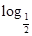 24)的值.
24)的值.
(1)求f(x)在[-1,0)上的解析式;
(2)求f(
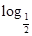 24)的值.
24)的值.(1)f(x)=-(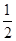 )x+1
)x+1
(2)-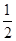
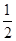 )x+1
)x+1(2)-
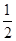
解:(1)令x∈[-1,0),则-x∈(0,1],
∴f(-x)=2-x-1.
又∵f(x)是奇函数,∴f(-x)=-f(x).
∴-f(x)=f(-x)=2-x-1.
∴f(x)=-(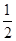 )x+1.
)x+1.
(2)∵f(x+2)=-f(x),
∴f(x+4)=-f(x+2)=f(x).
∴f(x)是以4为周期的周期函数.
∵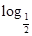 24=-log224∈(-5,-4),
24=-log224∈(-5,-4),
∴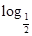 24+4∈(-1,0).
24+4∈(-1,0).
∴f(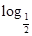 24)=f
24)=f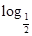 24+4)=-(
24+4)=-(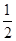 )
)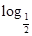 24+4+1=-24×
24+4+1=-24×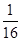 +1=-
+1=-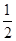 .
.
∴f(-x)=2-x-1.
又∵f(x)是奇函数,∴f(-x)=-f(x).
∴-f(x)=f(-x)=2-x-1.
∴f(x)=-(
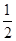 )x+1.
)x+1.(2)∵f(x+2)=-f(x),
∴f(x+4)=-f(x+2)=f(x).
∴f(x)是以4为周期的周期函数.
∵
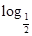 24=-log224∈(-5,-4),
24=-log224∈(-5,-4),∴
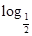 24+4∈(-1,0).
24+4∈(-1,0).∴f(
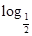 24)=f
24)=f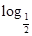 24+4)=-(
24+4)=-(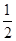 )
)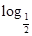 24+4+1=-24×
24+4+1=-24×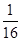 +1=-
+1=-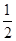 .
.
练习册系列答案
相关题目
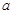 为实常数,
为实常数,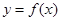 是定义在
是定义在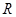 上的奇函数,当
上的奇函数,当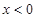 时,
时,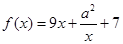 , 若
, 若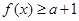 对一切
对一切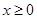 成立,则
成立,则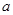 的取值范围为 .
的取值范围为 .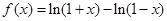 ,
,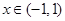 .现有下列命题:
.现有下列命题: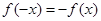 ;②
;②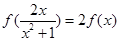 ;③
;③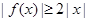 .其中的所有正确命题的序号是( )
.其中的所有正确命题的序号是( )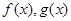 分别是定义在
分别是定义在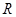 上的偶函数和奇函数,且
上的偶函数和奇函数,且 ,则
,则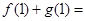
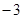
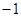
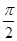 )=1,则f(-
)=1,则f(-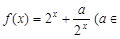 R)为奇函数,则
R)为奇函数,则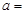 .
. ,则f(-1)=( )
,则f(-1)=( )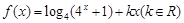 是偶函数.
是偶函数. 的值;
的值; ,若函数
,若函数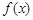 与
与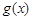 的图象有且只有一个公共点,求实数a的取值范围.
的图象有且只有一个公共点,求实数a的取值范围.