题目内容
4.已知函数f(x)=$\frac{-{2}^{x}+a}{{2}^{x+1}-b}$(a、b为实数,且a>0)是奇函数.(1)求a与b的值;
(2)解不等式f(log${\;}_{\frac{1}{3}}$x)+f(-1)>0.
分析 (1)利用f(x)是奇函数,f(0)=0,f(-1)+f(1)=0,求出a、b的值;
(2)由(1)得f(x)定义域上的减函数,把不等式f(log${\;}_{\frac{1}{3}}$x)+f(-1)>0化为${log}_{\frac{1}{3}}$x<1,求出解集即可.
解答 解:(1)∵函数f(x)=$\frac{-{2}^{x}+a}{{2}^{x+1}-b}$是奇函数,
∴f(0)=$\frac{-1+a}{2-b}$=0,
解得a=1;
又f(-1)+f(1)=$\frac{-\frac{1}{2}+1}{1-b}$+$\frac{-2+1}{{2}^{2}-b}$=$\frac{\frac{1}{2}b+1}{(1-b)(4-b)}$=0,
解得b=-2;
(2)由(1)得,f(x)=$\frac{{-2}^{x}+1}{{2}^{x+1}+2}$=-$\frac{1}{2}$+$\frac{1}{{2}^{x}+1}$是定义域上的减函数,
∴不等式f(log${\;}_{\frac{1}{3}}$x)+f(-1)>0可化为
f(${log}_{\frac{1}{3}}$x)>-f(-1)=f(1),
即${log}_{\frac{1}{3}}$x<1,
解得x>$\frac{1}{3}$;
∴该不等式的解集为{x|x>$\frac{1}{3}$}.
点评 本题考查了不等式的解法与应用问题,也考查了函数的性质与应用问题,是综合性题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.设i是虚数单位,在复平面内,复数z=2i(1+i)所对应的点落在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图为函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象.
如图为函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象.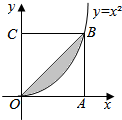
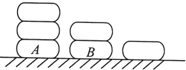 如图,桌面上摆有三串冰糖葫芦,第一串3课,第二串2颗,第三串1颗.小明每次从中取走一颗,若上面的冰糖葫芦取走后才能取下面的冰糖葫芦.则冰糖葫芦A恰好在第五次被取走,且冰糖葫芦B恰好在第六次被取走的取法数为12.
如图,桌面上摆有三串冰糖葫芦,第一串3课,第二串2颗,第三串1颗.小明每次从中取走一颗,若上面的冰糖葫芦取走后才能取下面的冰糖葫芦.则冰糖葫芦A恰好在第五次被取走,且冰糖葫芦B恰好在第六次被取走的取法数为12.