题目内容
15.方程$C_{11}^x=C_{11}^{2x-4}$的解为4或5.分析 根据组合数的性质,列出方程,求出方程的解.
解答 解:∵方程$C_{11}^x=C_{11}^{2x-4}$,
∴x=2x-4,或x+(2x-4)=11;
解得x=4或x=5,
经检验,x=4与x=5都是原方程的解.
故答案为:4或5.
点评 本题考查了组合数性质的应用问题,也考查了解方程的应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.函数f(x)=sin2x与函数g(x)=2x的图象的交点的个数是( )
| A. | 1 | B. | 3 | C. | 5 | D. | 7 |
6.圆(x-1)2+(y-2)2=1的圆心坐标是( )
| A. | (1,2) | B. | (-1,-2) | C. | (2,1) | D. | (-2,-1) |
7.已知△ABC的三个内角,A,B,C所对的边分别为a,b,c,若2cosBsinAsinC=sin2B,则( )
| A. | a,b,c成等差数列 | B. | $\sqrt{a}$,$\sqrt{b}$,$\sqrt{c}$成等比数列 | ||
| C. | a2,b2,c2成等差数列 | D. | a2,b2,c2成等比数列 |
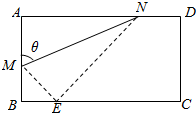 如图,折叠矩形纸片ABCD,使A点落在边BC上的E处,折痕的两端点M、N分别在线段AB和AD上(不与端点重合).已知AB=2,BC=$\frac{{4\sqrt{3}}}{3}$,设∠AMN=θ.
如图,折叠矩形纸片ABCD,使A点落在边BC上的E处,折痕的两端点M、N分别在线段AB和AD上(不与端点重合).已知AB=2,BC=$\frac{{4\sqrt{3}}}{3}$,设∠AMN=θ.