题目内容
12.已知△ABC的三个内角A,B,C所对的边分别为a,b,c,向量$\overrightarrow{m}$=(1,2),$\overrightarrow{n}$=(-1,cosA),且$\overrightarrow{m}•\overrightarrow{n}$=0.(Ⅰ)求角A的大小;
(Ⅱ)若a=$\sqrt{3}$,b+c=2$\sqrt{3}$,求证:△ABC为等边三角形.
分析 (Ⅰ)利用数量积公式求出A的余弦值,进而求角A的大小;
(Ⅱ)利用余弦定理得到a,b,c三边,判断三角形的形状.
解答 解:(Ⅰ)由向量$\overrightarrow{m}$=(1,2),$\overrightarrow{n}$=(-1,cosA),且$\overrightarrow{m}•\overrightarrow{n}$=0.
得到-1+2cosA=0解得cosA=$\frac{1}{2}$,由0<A<π,所以A=$\frac{π}{3}$;
(Ⅱ)证明:在△ABC中,因为a2=b2+c2-2bccosA,且a=$\sqrt{3}$,b+c=2$\sqrt{3}$,
所以3=b2+c2-2bc$•\frac{1}{2}$=b2+c2-bc=(b+c)2-3bc,解得c=$\sqrt{3}$,所以b=$\sqrt{3}$,
所以a=b=c=$\sqrt{3}$,所以三角形为等边三角形.
点评 本题考查了平面向量的数量积运用以及利用余弦定理判断三角形的形状;属于基础题目.

练习册系列答案
相关题目
7.已知△ABC的三个内角,A,B,C所对的边分别为a,b,c,若2cosBsinAsinC=sin2B,则( )
| A. | a,b,c成等差数列 | B. | $\sqrt{a}$,$\sqrt{b}$,$\sqrt{c}$成等比数列 | ||
| C. | a2,b2,c2成等差数列 | D. | a2,b2,c2成等比数列 |
17.${∫}_{0}^{1}$x2dx的值为( )
| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
7.抛物线x2=$\frac{1}{4}$y的准线方程是( )
| A. | y=1 | B. | y=-1 | C. | y=$\frac{1}{16}$ | D. | y=-$\frac{1}{16}$ |
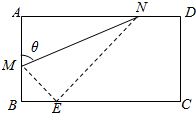 如图,折叠矩形纸片ABCD,使A点落在边BC上的E处,折痕的两端点M、N分别在线段AB和AD上(不与端点重合).已知AB=2,BC=$\frac{{4\sqrt{3}}}{3}$,设∠AMN=θ.
如图,折叠矩形纸片ABCD,使A点落在边BC上的E处,折痕的两端点M、N分别在线段AB和AD上(不与端点重合).已知AB=2,BC=$\frac{{4\sqrt{3}}}{3}$,设∠AMN=θ.