题目内容
9．
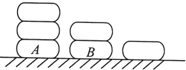如图，桌面上摆有三串冰糖葫芦，第一串3课，第二串2颗，第三串1颗．小明每次从中取走一颗，若上面的冰糖葫芦取走后才能取下面的冰糖葫芦．则冰糖葫芦A恰好在第五次被取走，且冰糖葫芦B恰好在第六次被取走的取法数为12．
分析 由题意可得，在前4次取走冰糖葫芦为，取走了A上面的2颗、取走了B上面的1颗，还取走了第三串1颗，根据位置，分为三类，根据分类计数原理可得．
解答 解：由题意可得，在前4次取走冰糖葫芦为，取走了A上面的2颗、取走了B上面的1颗，还取走了第三串1颗，
第一类，第一次先取第一串的最上面一颗，第二次，剩下的三颗任意去，故有A33=6种，
第二类，第一次先取第三串的一颗（或第二串的B上面的一颗），第二次取第一串的最上面一颗，第二次，剩下的二颗任意去，故有2×2=4种，
若三类，第一次二次先取第三串的一颗和第二串的B上面的一颗，剩下的二颗按从上到下的顺序取，故有2种，
根据分类计数原理，共有6+4+2=12种，
故答案为：12．
点评 本题考查了分类计数原理，关键是分类，属于中档题．
练习册系列答案
优学名师名题系列答案
相关题目
19．已知△ABC中，cosA=$\frac{2\sqrt{5}}{5}$，cosB=$\frac{3\sqrt{10}}{10}$，则内角C等于（ ）
| A． | $\frac{3π}{4}$ | B． | $\frac{2π}{3}$ | C． | $\frac{π}{2}$ | D． | $\frac{π}{4}$ |
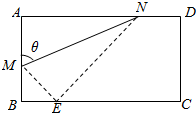如图，折叠矩形纸片ABCD，使A点落在边BC上的E处，折痕的两端点M、N分别在线段AB和AD上（不与端点重合）．已知AB=2，BC=$\frac{{4\sqrt{3}}}{3}$，设∠AMN=θ．
17．${∫}_{0}^{1}$x2dx的值为（ ）
| A． | $\frac{1}{3}$ | B． | 1 | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |