题目内容
2.四面体SABC,SA,SB,SC两两垂直,AB=4,BC=5,AC=6,SA与BC间的距离为$\frac{3}{2}$.分析 作出SA与BC间的距离,利用勾股定理以及解三角形求解即可.
解答 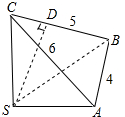 解:四面体S-ABC中,SA,SB,SC两两垂直,
解:四面体S-ABC中,SA,SB,SC两两垂直,
可知SA⊥平面SBC,过S在平面SBC作SD⊥BC于D,
则SD就是SA与BC间的距离.
AB=4,BC=5,AC=6,
可得:SA2+SC2=36,SA2+SB2=16,SB2+SC2=25,
SA2+SC2+SB2=$\frac{77}{2}$,
解得:SC=$\frac{\sqrt{10}}{2}$
SB=$\frac{3\sqrt{10}}{2}$,
SA=$\frac{3\sqrt{6}}{2}$,
∴SD=$\frac{SB•CS}{BC}$=$\frac{\frac{3\sqrt{10}}{2}×\frac{\sqrt{10}}{2}}{5}$=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题考查几何体的特征,异面直线的距离的求法,考查这思想以及空间想象能力计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.设0<x<1,0<y<1,且x≠y,则x+y,2$\sqrt{xy}$,x2+y2,2xy中,最大的一个是( )
| A. | 2xy | B. | 2$\sqrt{xy}$ | C. | x2+y2 | D. | x+y |
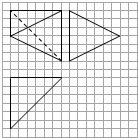 已知某几何体的三视图如图所示,求该几何体的体积.
已知某几何体的三视图如图所示,求该几何体的体积.