题目内容
1.若函数f(x)为奇函数且在(0,+∞)上为增函数,f(3)=0,则不等式子$\frac{f(x)-f(-x)}{x}$<0的解集是(-3,0)∪(0,3).分析 根据函数为奇函数求出f(3)=0,再将不等式化为$\frac{f(x)}{x}$<0,分成两类加以讨论,再分别利用函数的单调性进行求解,可以得出相应的解集.
解答 解:∵f(x)为奇函数,且在(0,+∞)上是增函数,f(3)=0,
∴f(-x)=-f(x),
即有f(-3)=-f(3)=0,在(-∞,0)内是增函数.
∴$\frac{f(x)-f(-x)}{x}$<0,即为$\frac{f(x)}{x}$<0,
则$\left\{\begin{array}{l}{x>0}\\{f(x)<0=f(3)}\end{array}\right.$或$\left\{\begin{array}{l}{x<0}\\{f(x)>0=f(-3)}\end{array}\right.$,
根据在(-∞,0)和(0,+∞)内是都是增函数,
解得:x∈(-3,0)∪(0,3)
故答案为:(-3,0)∪(0,3).
点评 本题主要考查了函数的奇偶性的性质,以及函数单调性的应用等有关知识,属于中档题.结合函数的草图,会对此题有更深刻的理解.

练习册系列答案
相关题目
16.函数y=f(x)的图象如图,则f(x)的定义域是( )
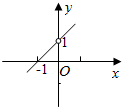
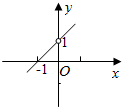
| A. | R | B. | (-∞,1)∪(1,+∞) | C. | (-∞,0)∪(0,+∞) | D. | (-1,0) |
6.已知A={x|-1<x<3},B={x|0<x<4},C={x|m<x<5},若(A∩B)∪C={x|0<x<5},则实数m的取值范围为( )
| A. | 0<m<3 | B. | 0<m<5 | C. | 0≤m<5 | D. | 0≤m<3 |