题目内容
5.用多种方法求函数y=2x+$\sqrt{x-1}$最小值.(换元法或单调性)分析 换元,利用配方法,结合函数的单调性,即可求出函数的最小值;单调性法:由y=2x及y=$\sqrt{x-1}$同时在x≥1递增,知道y=2x+$\sqrt{x-1}$在x≥1也递增,即可求出函数的最小值.
解答 解:用换元法,令$\sqrt{x-1}$=t,则x=t2+1(t≥0),
y=2(t2+1)+t=2(t+$\frac{1}{4}$)2+$\frac{15}{8}$,
∵t≥0,
∴函数在[0,+∞)上单调递增,
∴t=0时,函数取得最小值2;
单调性法:由y=2x及y=$\sqrt{x-1}$同时在x≥1递增,知道y=2x+$\sqrt{x-1}$在x≥1也递增,
∴在x=1时最小值是x=1时y=2×1+0=2.
点评 本题考查函数的最小值,考查换元法,考查函数的单调性,属于中档题.

练习册系列答案
相关题目
16.函数y=f(x)的图象如图,则f(x)的定义域是( )
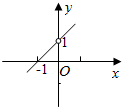
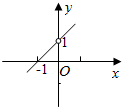
| A. | R | B. | (-∞,1)∪(1,+∞) | C. | (-∞,0)∪(0,+∞) | D. | (-1,0) |
7.在约束条件$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{y+x≤4}\\{y+2x≤s}\end{array}\right.$下,当2≤s≤8时,目标函数z=3x+2y的最大值的变化范围是( )
| A. | [3,12] | B. | [4,12] | C. | [3,8] | D. | [6,12] |
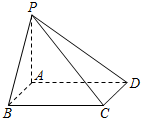 如图,在四棱锥P-ABCD中,底面正方形ABCD为边长为2,PA⊥底面ABCD,E为BC的中点,PC与平面PAD所成的角为arctan$\frac{{\sqrt{2}}}{2}$.
如图,在四棱锥P-ABCD中,底面正方形ABCD为边长为2,PA⊥底面ABCD,E为BC的中点,PC与平面PAD所成的角为arctan$\frac{{\sqrt{2}}}{2}$.