题目内容
16.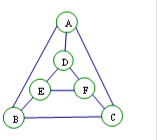 执行某个程序,电脑会随机地按如下要求给图中六个小圆涂色.
执行某个程序,电脑会随机地按如下要求给图中六个小圆涂色.①有五种给定的颜色供选用;
②每个小圆涂一种颜色,且图中被同一条线段相连两个小圆不能涂相同的颜色.
若电脑完成每种涂色方案的可能形相同,则执行一次程序后,图中刚好有四种不同的颜色的概率是( )
| A. | $\frac{9}{16}$ | B. | $\frac{3}{8}$ | C. | $\frac{18}{25}$ | D. | $\frac{12}{25}$ |
分析 分别讨论满足条件的涂色的总数,以及刚好有四种不同的颜色的数目,利用概率公式进行求解即可.
解答 解:分两步来进行,先涂A、B、C,再涂D、E、F.
①若5种颜色都用上,先涂A、B、C,方法有${A}_{5}^{3}$种;再涂D、E、F中的两个点,方法有${A}_{3}^{2}$种,
最后剩余的一个点只有2种涂法,故此时方法共有${A}_{5}^{3}$•${A}_{3}^{2}$•2=720种.
②若5种颜色只用4种,首先选出4种颜色,方法有${C}_{5}^{4}$种;
先涂A、B、C,方法有${A}_{4}^{3}$种;再涂D、E、F中的1个点,方法有3种,
最后剩余的两个点只有3种涂法,故此时方法共有${C}_{5}^{4}$•${A}_{4}^{3}$•3•3=1080种.
③若5种颜色只用3种,首先选出3种颜色,方法有${C}_{5}^{3}$种;
先涂A、B、C,方法有${A}_{3}^{3}$种;再涂D、E、F,方法有2种,
故此时方法共有 ${C}_{5}^{3}$•${A}_{3}^{3}$•2=120 种.
综上可得,不同涂色方案共有 720+1080+120=1920 种,
则图中刚好有四种不同的颜色的概率是$\frac{1080}{1920}$=$\frac{9}{16}$.
故选:A
点评 本题主要考查古典概型的概率的计算,利用排列组合的基础知识与分类讨论思想是解决本题的关键.难度较大.

练习册系列答案
相关题目
8.某单位对三个车间的人数统计情况如表:用分层抽样的方法从三个车间抽取30人,其中三车间有12人.
(Ⅰ)求k的值;
(Ⅱ)为了考察职工加班情况,从编号000~199中的一车间男职工中,用系统抽样法先后抽取5人的全年加班天数分别为75,79,82,73,81.已知73对应的编号为145,75对应的编号是多少?并求这五个人加班天数的方差.
(Ⅰ)求k的值;
(Ⅱ)为了考察职工加班情况,从编号000~199中的一车间男职工中,用系统抽样法先后抽取5人的全年加班天数分别为75,79,82,73,81.已知73对应的编号为145,75对应的编号是多少?并求这五个人加班天数的方差.
| 一车间 | 二车间 | 三车间 | |
| 男职工 | 200 | 100 | 250 |
| 女职工 | 600 | k | 550 |
5.设数列{an},{bn}都是等比数列,且a1=25,b1=4,a2•b2=100,那么数列{an•bn}的第37项的值是( )
| A. | 1 | B. | 37 | C. | 100 | D. | -37 |
 如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC,E为BC的中点,F在棱AC上,且AF=3FC,M为AD上一点且AM=2DM.
如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC,E为BC的中点,F在棱AC上,且AF=3FC,M为AD上一点且AM=2DM.