题目内容
8.某单位对三个车间的人数统计情况如表:用分层抽样的方法从三个车间抽取30人,其中三车间有12人.(Ⅰ)求k的值;
(Ⅱ)为了考察职工加班情况,从编号000~199中的一车间男职工中,用系统抽样法先后抽取5人的全年加班天数分别为75,79,82,73,81.已知73对应的编号为145,75对应的编号是多少?并求这五个人加班天数的方差.
| 一车间 | 二车间 | 三车间 | |
| 男职工 | 200 | 100 | 250 |
| 女职工 | 600 | k | 550 |
分析 (Ⅰ)根据分层抽样的定义建立比例关系即可得到结论.
(Ⅱ)根据系统抽样的定义进行求解即可.
解答 解:( I)由题意得$\frac{12}{30}=\frac{800}{k+1700}$,解得k=300.----------------------(3分)
( II)由题意得,抽取间距d=$\frac{200}{5}=40$,----------------------(4分)
设7的编号是m,
则145=m+(4-1)×40,
解得m=25
所以75对应的编号是25.----------------------(6分)
$\overline{x}$=$\frac{1}{5}$(75+79+82+73+81)=78;----------------------(9分)
s2=$\frac{1}{5}$[(75-78)2+(79-78)2+(82-78)2+(73-78)2+(81-78)2]=12----(12分)
点评 本题主要考查样本平均数和方差的计算以及分层抽样,系统抽样的应用,根据相应的公式是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.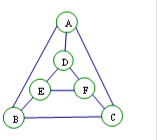 执行某个程序,电脑会随机地按如下要求给图中六个小圆涂色.
执行某个程序,电脑会随机地按如下要求给图中六个小圆涂色.
①有五种给定的颜色供选用;
②每个小圆涂一种颜色,且图中被同一条线段相连两个小圆不能涂相同的颜色.
若电脑完成每种涂色方案的可能形相同,则执行一次程序后,图中刚好有四种不同的颜色的概率是( )
 执行某个程序,电脑会随机地按如下要求给图中六个小圆涂色.
执行某个程序,电脑会随机地按如下要求给图中六个小圆涂色.①有五种给定的颜色供选用;
②每个小圆涂一种颜色,且图中被同一条线段相连两个小圆不能涂相同的颜色.
若电脑完成每种涂色方案的可能形相同,则执行一次程序后,图中刚好有四种不同的颜色的概率是( )
| A. | $\frac{9}{16}$ | B. | $\frac{3}{8}$ | C. | $\frac{18}{25}$ | D. | $\frac{12}{25}$ |
20.“x>3”是“x>2”的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.已知a=($\frac{1}{5}$)-2,b=log5${\;}{\frac{1}{3}}$,c=log53,则a,b,c的大小关系是( )
| A. | a>b>c | B. | c>a>b | C. | a>c>b | D. | c>b>a |
18.已知F1,F2是双曲线的两个焦点,P,Q是过点F1且垂直于实轴所在直线的双曲线的弦,∠PF2Q=90°,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{2}+1$ | C. | $\sqrt{2}-1$ | D. | $\frac{{\sqrt{2}}}{2}+1$ |