题目内容
11. 如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC,E为BC的中点,F在棱AC上,且AF=3FC,M为AD上一点且AM=2DM.
如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC,E为BC的中点,F在棱AC上,且AF=3FC,M为AD上一点且AM=2DM.(1)求证:AC⊥平面DEF;
(2)求证:BM∥平面DEF.
分析 (1)取AC的中点H,要证明AC⊥平面DEF,可先证DE⊥AC,再证明EF⊥AC即可.
(2)先证明MH∥DF,又EF∥BH,EF∩DF=F,BH∩MH=H,从而可证平面DEF∥平面MHB,即可证明BM∥平面DEF.
解答 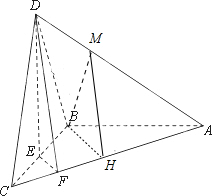 证明:(1)取AC的中点H,∵AB=BC,∴BH⊥AC.
证明:(1)取AC的中点H,∵AB=BC,∴BH⊥AC.
∵AF=3FC,∴F为CH的中点.
∵E为BC的中点,∴EF∥BH.则EF⊥AC.
∵△BCD是正三角形,∴DE⊥BC.
∵AB⊥平面BCD,∴AB⊥DE.
∵AB∩BC=B,∴DE⊥平面ABC.∴DE⊥AC.
∵DE∩EF=E,∴AC⊥平面DEF.
(2)∵△BCD是正三角形,AB⊥平面BCD,
∴AD=BC,
∵M为AD上一点且AM=2DM.F在棱AC上,且AF=3FC,且H为AC的中点,
∴$\frac{AM}{MD}=\frac{AH}{HF}$=2,
∴MH∥DF,
又∵EF∥BH,EF∩DF=F,BH∩MH=H,
∴平面DEF∥平面MHB,
∴BM∥平面DEF.
点评 本题主要考查了直线与平面垂直的判定,直线与平面平行的判定,考查了空间想象能力和推理论证能力,属于中档题.

练习册系列答案
相关题目
8.若直线y=kx+1与圆x2+y2=1相交与P,Q两点,且此圆被分成的两段弧长之比为1:2,则k的值为( )
| A. | $-\sqrt{3}$或$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $-\sqrt{2}$或$\sqrt{2}$ | D. | $\sqrt{2}$ |
16.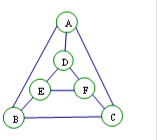 执行某个程序,电脑会随机地按如下要求给图中六个小圆涂色.
执行某个程序,电脑会随机地按如下要求给图中六个小圆涂色.
①有五种给定的颜色供选用;
②每个小圆涂一种颜色,且图中被同一条线段相连两个小圆不能涂相同的颜色.
若电脑完成每种涂色方案的可能形相同,则执行一次程序后,图中刚好有四种不同的颜色的概率是( )
 执行某个程序,电脑会随机地按如下要求给图中六个小圆涂色.
执行某个程序,电脑会随机地按如下要求给图中六个小圆涂色.①有五种给定的颜色供选用;
②每个小圆涂一种颜色,且图中被同一条线段相连两个小圆不能涂相同的颜色.
若电脑完成每种涂色方案的可能形相同,则执行一次程序后,图中刚好有四种不同的颜色的概率是( )
| A. | $\frac{9}{16}$ | B. | $\frac{3}{8}$ | C. | $\frac{18}{25}$ | D. | $\frac{12}{25}$ |
20.“x>3”是“x>2”的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
