题目内容
1．给出下列四个命题：（1）对于任意的n＞4，n∈Z，2n＞n2
（2）对于任意实数a，b，总有2（a2+b2）≥（a+b）2
（3）$\sqrt{3}$+$\sqrt{7}$＜2$\sqrt{5}$
（4）平面内的4条直线，最多将平面分割成11部分．
这四个命题中，真命题的序号为（1）、（2）、（3）、（4）．
分析 （1）n＞4，且n∈Z时，2n＞n2恒成立；
（2）由基本不等式得出a2+b2≥2ab，从而得2（a2+b2）≥（a+b）2成立；
（3）用分析法证明$\sqrt{3}$+$\sqrt{7}$＜2$\sqrt{5}$成立；
（4）画图表示平面内的4条直线，最多将平面分割成11部分．
解答 解：对于（1），任意的n＞4，n∈Z，都有2n＞n2，
∴命题（1）正确；
对于（2），任意实数a，b，总有a2+b2≥2ab，
∴2（a2+b2）≥a2+b2+2ab=（a+b）2，
∴命题（2）正确；
对于（3），若$\sqrt{3}$+$\sqrt{7}$＜2$\sqrt{5}$，则3+7+2$\sqrt{3×7}$＜${（2\sqrt{5}）}^{2}$，
即$\sqrt{21}$＜5，
∴21＜25，
∴命题（3）成立；
对于（4），平面内的4条直线，最多将平面分割成11部分，如图所示；
∴命题（4）正确．
综上，以上正确的命题是（1）、（2）、（3）、（4）．
故答案为：（1）、（2）、（3）、（4）．
点评 本题考查了指数函数与幂函数的应用问题，也考查了基本不等式的应用问题，考查了不等式的证明与应用问题，考查了空间想象能力的应用问题，是综合性题目．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
相关题目
16．
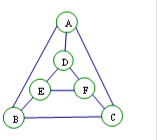执行某个程序，电脑会随机地按如下要求给图中六个小圆涂色．
①有五种给定的颜色供选用；
②每个小圆涂一种颜色，且图中被同一条线段相连两个小圆不能涂相同的颜色．
若电脑完成每种涂色方案的可能形相同，则执行一次程序后，图中刚好有四种不同的颜色的概率是（ ）
执行某个程序，电脑会随机地按如下要求给图中六个小圆涂色．①有五种给定的颜色供选用；
②每个小圆涂一种颜色，且图中被同一条线段相连两个小圆不能涂相同的颜色．
若电脑完成每种涂色方案的可能形相同，则执行一次程序后，图中刚好有四种不同的颜色的概率是（ ）
| A． | $\frac{9}{16}$ | B． | $\frac{3}{8}$ | C． | $\frac{18}{25}$ | D． | $\frac{12}{25}$ |
