题目内容
6.设函数f(x)是定义在R上的偶函数,且对任意的x∈R恒有f(x+1)=f(x-1),已知当x∈[0,1]时f(x)=($\frac{1}{2}$)1-x,则①2是函数f(x)的周期;
②函数f(x)在(1,2)上是减函数,在(2,3)上是增函数;
③函数f(x)的最大值是1,最小值是0;
④当x∈(3,4)时,f(x)=($\frac{1}{2}$)x-3.
其中所有正确命题的序号是①②④.
分析 根据条件求出函数的周期,即可判定①的真假,根据函数f(x)是定义在R上的偶函数,以及在(0,1)上的单调性,可判定②的真假,根据单调性和周期性可求出函数的最值,可判定③的真假,最后求出函数在x∈[3,4]时的解析式即可判定④的真假
解答 解:∵对任意的x∈R恒有f(x+1)=f(x-1),
∴f(x+2)=f(x)则f(x)的周期为2,故①正确;
∵函数f(x)是定义在R上的偶函数,当x∈[0,1]时,f(x)=($\frac{1}{2}$)1-x,
∴函数f(x)在(0,1)上是增函数,函数f(x)在(1,2)上是减函数,在(2,3)上是增函数,故②正确;
∴函数f(x)的最大值是f(1)=1,最小值为f(0)=$\frac{1}{2}$,故③不正确;
设x∈[3,4],则4-x∈[0,1],f(4-x)=($\frac{1}{2}$)x-3=f(-x)=f(x),故④正确
故答案为:①②④
点评 本题考查函数的奇偶性、周期性、单调性以及函数的最值,同时考查了分析问题的能力,是中档题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
16.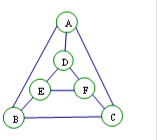 执行某个程序,电脑会随机地按如下要求给图中六个小圆涂色.
执行某个程序,电脑会随机地按如下要求给图中六个小圆涂色.
①有五种给定的颜色供选用;
②每个小圆涂一种颜色,且图中被同一条线段相连两个小圆不能涂相同的颜色.
若电脑完成每种涂色方案的可能形相同,则执行一次程序后,图中刚好有四种不同的颜色的概率是( )
 执行某个程序,电脑会随机地按如下要求给图中六个小圆涂色.
执行某个程序,电脑会随机地按如下要求给图中六个小圆涂色.①有五种给定的颜色供选用;
②每个小圆涂一种颜色,且图中被同一条线段相连两个小圆不能涂相同的颜色.
若电脑完成每种涂色方案的可能形相同,则执行一次程序后,图中刚好有四种不同的颜色的概率是( )
| A. | $\frac{9}{16}$ | B. | $\frac{3}{8}$ | C. | $\frac{18}{25}$ | D. | $\frac{12}{25}$ |
17.已知a=($\frac{1}{5}$)-2,b=log5${\;}{\frac{1}{3}}$,c=log53,则a,b,c的大小关系是( )
| A. | a>b>c | B. | c>a>b | C. | a>c>b | D. | c>b>a |
14.在△ABC中,若BC=2,AC=1,∠A=30°,则△ABC是( )
| A. | 钝角三角形 | B. | 锐角三角形 | C. | 直角三角形 | D. | 形状不能确定 |
18.已知F1,F2是双曲线的两个焦点,P,Q是过点F1且垂直于实轴所在直线的双曲线的弦,∠PF2Q=90°,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{2}+1$ | C. | $\sqrt{2}-1$ | D. | $\frac{{\sqrt{2}}}{2}+1$ |
16.已知数列{an}满足an+1=$\frac{1}{{1-{a_n}}}$,若a1=$\frac{1}{2}$,则a2015=( )
| A. | 2 | B. | -2 | C. | -1 | D. | $\frac{1}{2}$ |