题目内容
5.设数列{an},{bn}都是等比数列,且a1=25,b1=4,a2•b2=100,那么数列{an•bn}的第37项的值是( )| A. | 1 | B. | 37 | C. | 100 | D. | -37 |
分析 根据等比数列的性质和通项公式进行求解即可.
解答 解:∵数列{an},{bn}都是等比数列,
∴设数列{an},{bn}的公比分别为q,p,
则当n≥2时,$\frac{{a}_{n}•{b}_{n}}{{a}_{n-1}•{b}_{n-1}}$=pq为常数,
即么数列{an•bn}也是等比数列,
∵a1=25,b1=4,a2•b2=100,
∴数列{an•bn}的公比pq=$\frac{{a}_{2}{b}_{2}}{{a}_{1}{b}_{1}}$=$\frac{100}{25×4}=1$,
则数列{an•bn}的第37项等于a2•b2=100,
故选:C
点评 本题主要考查等比数列的判断以及等比数列通项公式的应用,根据等比数列的性质判断数列{an•bn}也是等比数列是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.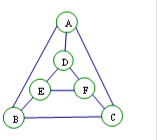 执行某个程序,电脑会随机地按如下要求给图中六个小圆涂色.
执行某个程序,电脑会随机地按如下要求给图中六个小圆涂色.
①有五种给定的颜色供选用;
②每个小圆涂一种颜色,且图中被同一条线段相连两个小圆不能涂相同的颜色.
若电脑完成每种涂色方案的可能形相同,则执行一次程序后,图中刚好有四种不同的颜色的概率是( )
 执行某个程序,电脑会随机地按如下要求给图中六个小圆涂色.
执行某个程序,电脑会随机地按如下要求给图中六个小圆涂色.①有五种给定的颜色供选用;
②每个小圆涂一种颜色,且图中被同一条线段相连两个小圆不能涂相同的颜色.
若电脑完成每种涂色方案的可能形相同,则执行一次程序后,图中刚好有四种不同的颜色的概率是( )
| A. | $\frac{9}{16}$ | B. | $\frac{3}{8}$ | C. | $\frac{18}{25}$ | D. | $\frac{12}{25}$ |
20.“x>3”是“x>2”的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.已知a=($\frac{1}{5}$)-2,b=log5${\;}{\frac{1}{3}}$,c=log53,则a,b,c的大小关系是( )
| A. | a>b>c | B. | c>a>b | C. | a>c>b | D. | c>b>a |
14.在△ABC中,若BC=2,AC=1,∠A=30°,则△ABC是( )
| A. | 钝角三角形 | B. | 锐角三角形 | C. | 直角三角形 | D. | 形状不能确定 |
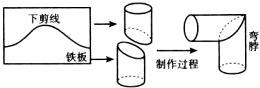 铁匠师傅在打制烟筒弯脖时,为确保对接成直角,在铁板上的下剪线正好是余弦曲线$y=acos\frac{x}{a}$的一个周期的图象如图,当弯脖的直径为12cm时,a应是6cm.
铁匠师傅在打制烟筒弯脖时,为确保对接成直角,在铁板上的下剪线正好是余弦曲线$y=acos\frac{x}{a}$的一个周期的图象如图,当弯脖的直径为12cm时,a应是6cm.