题目内容
 如图所示,四面体ABCD中,AB⊥BD、AC⊥CD且AD=3,BD=CD=2.
如图所示,四面体ABCD中,AB⊥BD、AC⊥CD且AD=3,BD=CD=2.(1)求证:AD⊥BC;
(2)求二面角B-AC-D的余弦值.
考点:二面角的平面角及求法,棱锥的结构特征
专题:空间位置关系与距离,空间角
分析:(1)作AH⊥平面BCD于H,连接BH、CH、DH,由已知得四边形BHCD是正方形,且AH=1,以D为原
点,以DB所在直线为x轴,DC所在直线为y轴,以垂直于DB,DC的直线为z轴,建立空间直角坐标系,利用向量法能证明AD⊥BC.
(2)求出平面ABC的法向量的平面ACD的法向量,利用向量法能求出二面角B-AC-D的余弦值.
点,以DB所在直线为x轴,DC所在直线为y轴,以垂直于DB,DC的直线为z轴,建立空间直角坐标系,利用向量法能证明AD⊥BC.
(2)求出平面ABC的法向量的平面ACD的法向量,利用向量法能求出二面角B-AC-D的余弦值.
解答:
(1)证明 作AH⊥平面BCD于H,连接BH、CH、DH,
由已知得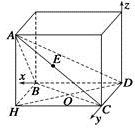 四边形BHCD是正方形,且AH=1,以D为原
四边形BHCD是正方形,且AH=1,以D为原
点,以DB所在直线为x轴,DC所在直线为y轴,
以垂直于DB,DC的直线为z轴,建立空间直角坐
标系,如图所示,则B(2,0,0),
C(0,2,0),D(0,0,0)A(2,2,1),
所以
=(-2,2,0),
=(0,2,0),
=(-2,0,-1),
=(2,2,1),
因此
•
=-4+4=0,所以AD⊥BC.
(2)解:设平面ABC的法向量为
=(x,y,z),
则由
1⊥
知:
•
=-2x+2y=0,
同理由
⊥
知:
•
=-2x-z=0,
可取
=(1,1,-2),
同理,可求得平面ACD的一个法向量为
=(1,0,2),
∴cos<
,
>=
=
,
即二面角B-AC-D的余弦值为
.
由已知得
 四边形BHCD是正方形,且AH=1,以D为原
四边形BHCD是正方形,且AH=1,以D为原点,以DB所在直线为x轴,DC所在直线为y轴,
以垂直于DB,DC的直线为z轴,建立空间直角坐
标系,如图所示,则B(2,0,0),
C(0,2,0),D(0,0,0)A(2,2,1),
所以
| BC |
| DC |
| AC |
| DA |
因此
| BC |
| DA |
(2)解:设平面ABC的法向量为
| n1 |
则由
| n1 |
| BC |
| n1 |
| BC |
同理由
| n1 |
| AC |
| n1 |
| AC |
可取
| n1 |
同理,可求得平面ACD的一个法向量为
| n2 |
∴cos<
| n1 |
| n2 |
| 1+4 | ||||
|
| ||
| 6 |
即二面角B-AC-D的余弦值为
| ||
| 6 |
点评:本题考查线面垂直,考查面面角,解题的关键是掌握线面垂直的判定方法,正确运用向量法解决面面角问题.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
要得到函数y=cos(2x-
)的图象,只需将函数y=cos(2x+
)的图象( )
| 2π |
| 3 |
| π |
| 3 |
A、向右平移
| ||
B、向左平移
| ||
C、向左平移
| ||
D、向右平移
|
(文)现有四个函数:①y=x•sinx;②y=x•cosx;③y=x|cosx|;④y=x•2x的图象(部分)如图:

则按照从左到右图象对应的函数序号安排正确的一组是( )

则按照从左到右图象对应的函数序号安排正确的一组是( )
| A、①④③② | B、③④②① |
| C、④①②③ | D、①④②③ |
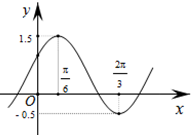 已知函数y=Asin(ωx+φ)+b的一部分图象如图所示,若A>0,ω>0,|φ|<
已知函数y=Asin(ωx+φ)+b的一部分图象如图所示,若A>0,ω>0,|φ|< 如图,E,F是边长为3的正方形ABCD的边AD上两个点,且AE=DF.连接CF交BD于G,连接BE交AG于点H,若|CH|2:|CE|2=9:10,则AE的长为
如图,E,F是边长为3的正方形ABCD的边AD上两个点,且AE=DF.连接CF交BD于G,连接BE交AG于点H,若|CH|2:|CE|2=9:10,则AE的长为