题目内容
8.求证:以抛物线y2=2px(p>0)上的任意不同的四点为顶点的四边形不可能是平行四边形.分析 假设抛物线上任意不同的四点为顶点的四边形ABCD是平行四边形.设抛物线上的四个点为A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),运用点满足方程和直线的斜率公式,可得AB,BC,CD,DA的斜率,再由平行线可得斜率相等,进而得到A,C,重合,B,D重合,得到矛盾,即可得证.
解答 证明:假设抛物线上任意不同的四点为顶点的四边形ABCD是平行四边形.
设抛物线上的四个点为A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
即有yi2=2pxi,即xi=$\frac{{{y}_{i}}^{2}}{2p}$(i=1,2,3,4),
于是kAB=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$=$\frac{2p}{{y}_{1}+{y}_{2}}$,
同理可得kBC=$\frac{2p}{{y}_{2}+{y}_{3}}$,kCD=$\frac{2p}{{y}_{3}+{y}_{4}}$,kAD=$\frac{2p}{{y}_{1}+{y}_{4}}$,
由假设可得kAB=kCD,kBC=kAD,从而y1=y3,y2=y4,
进而可得x1=x3,x2=x4,于是A,C重合,B,D重合,
这与A,B,C,D为抛物线上不同的四个点矛盾,所以假设不成立.
故抛物线y2=2px(p>0)上的任意不同的四点为顶点的四边形不可能是平行四边形
点评 本题考查抛物线的方程的运用,考查反证法的运用,以及推理能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.设a=log0.32,b=log32,c=20.3,则这三个数的大小关系是( )
| A. | b>c>a | B. | a>c>b | C. | a>b>c | D. | c>b>a |
3.函数f(x)=$\frac{{a}^{x+1}+{b}^{x+1}}{{a}^{x}+{b}^{x}}$(a>0,b>0,a≠b)在R上的单调性为( )
| A. | 增函数 | B. | 减函数 | C. | 不增不减函数 | D. | 与a,b的取值有关 |
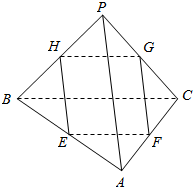 如图所示,在三棱锥P-ABC中,PA=4,BC=6,与PA、BC都平行的截面四边形EFGH的周长为l,试确定l的取值范围.
如图所示,在三棱锥P-ABC中,PA=4,BC=6,与PA、BC都平行的截面四边形EFGH的周长为l,试确定l的取值范围.