题目内容
19.已知函数f(x)=a-$\frac{2}{{2}^{x}+1}$是奇函数(a∈R).(1)求实数a的值;
(2)求函数y=f(x)的值域;
(3)试判断函数f(x)在(-∞,+∞)上的单调性,并用定义证明你的结论.
分析 (1)利用f(x)是奇函数,f(-x)=-f(x),即可求实数a的值;
(2)f(x)=1-$\frac{2}{{2}^{x}+1}$,即可求函数y=f(x)的值域;
(3)利用单调性定义证明结论.
解答 解:(1)由题意可得:f(x)=$\frac{a•{2}^{x}+a-2}{{2}^{x}+1}$
∵f(x)是奇函数,∴f(-x)=-f(x)
即$\frac{a•{2}^{-x}+a-2}{{2}^{-x}+1}$=-$\frac{a•{2}^{x}+a-2}{{2}^{x}+1}$
∴a-2=-a,即a=1
即f(x)=1-$\frac{2}{{2}^{x}+1}$; (3分)
(2)f(x)=1-$\frac{2}{{2}^{x}+1}$,${2^x}+1>1∴\frac{2}{{{2^x}+1}}∈({0,2})$,∴f(x)∈(-1,1)(6分)
(3)设x1,x2为区间(-∞,+∞)内的任意两个值,且x1<x2,
则0<${2}^{{x}_{1}}$<${2}^{{x}_{2}}$,${2}^{{x}_{1}}$-${2}^{{x}_{2}}$<0,
∵f(x1)-f(x2)=$\frac{2({2}^{{x}_{1}}-{2}^{{x}_{2}})}{({2}^{{x}_{1}}+1)({2}^{{x}_{2}}+1)}$<0
即f(x1)<f(x2),
∴f(x)是(-∞,+∞)上的增函数.(12分)
点评 本题考查了函数的奇偶性、单调性、指数函数的运算,考查了计算能力,属于中档题.

练习册系列答案
相关题目
10.函数f(x)=ln$\frac{3x}{2}-\frac{2}{x}$,则函数f(x)的零点所在区间为( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
4.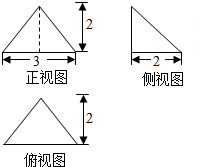 若某多面体的三视图如图所示,则此多面体的表面积是( )
若某多面体的三视图如图所示,则此多面体的表面积是( )
 若某多面体的三视图如图所示,则此多面体的表面积是( )
若某多面体的三视图如图所示,则此多面体的表面积是( )| A. | 6 | B. | 18 | C. | 8+3$\sqrt{2}$ | D. | 3+4$\sqrt{13}$ |