题目内容
 如图,在四棱锥V-ABCD中,四边形ABCD的对角线AC,BD相交于点O,已知底面ABCD是边长为2的正方形,其它四个侧面都是侧棱长为
如图,在四棱锥V-ABCD中,四边形ABCD的对角线AC,BD相交于点O,已知底面ABCD是边长为2的正方形,其它四个侧面都是侧棱长为| 5 |
(1)求二面角V-BC-A的平面角的大小.
(2)求点O到平面VBC的距离;
(3)求VV-ABCD.
考点:点、线、面间的距离计算,棱柱、棱锥、棱台的体积,二面角的平面角及求法
专题:空间位置关系与距离,空间角
分析:(1)取BC的中点E,连接EO,VE,VO,由正四棱锥的性质易得∠VEO为二面角V-BC-A的平面角,
(2)过O作OF⊥VE于F,即得点O到平面VBC的距离的大小.
(3)求出高VO,根据四棱锥的体积公式即可得到结论.
(2)过O作OF⊥VE于F,即得点O到平面VBC的距离的大小.
(3)求出高VO,根据四棱锥的体积公式即可得到结论.
解答:
解:(1)取BC的中点E,连接EO,VE,VO,则由题意可知VE⊥BC且OE⊥BC,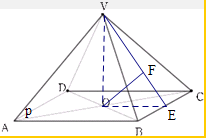
∴∠VEO为二面角V-BC-A的平面角,
∵VA=VB=VC=VD=
,O是底面正方形ABCD的中心,
∴VO⊥平面ABCD
Rt△VEO中,DE=1,BE=1,VE=2
可得∠VEO=60°
∴二面角V-BC-A的大小为60°
(2)设点O到平面VBC的距离为h,
过O作OF⊥VE于F,
则OF⊥平面VBC,
即OF是点O到平面VBC的距离,
则Rt△VEO中,OF=OEsin60°=
.
(3)由(2)知,VO=
=
=
,
故VV-ABCD=
×22×
=
.

∴∠VEO为二面角V-BC-A的平面角,
∵VA=VB=VC=VD=
| 5 |
∴VO⊥平面ABCD
Rt△VEO中,DE=1,BE=1,VE=2
可得∠VEO=60°
∴二面角V-BC-A的大小为60°
(2)设点O到平面VBC的距离为h,
过O作OF⊥VE于F,
则OF⊥平面VBC,
即OF是点O到平面VBC的距离,
则Rt△VEO中,OF=OEsin60°=
| ||
| 2 |
(3)由(2)知,VO=
| VE2-OE2 |
| 4-1 |
| 3 |
故VV-ABCD=
| 1 |
| 3 |
| 3 |
4
| ||
| 3 |
点评:本题给出正四棱锥,求侧面与底面所成角的大小,并求底面中心到一个侧面的距离,着重考查了二面角的平面角及求法和点到平面距离求法等知识,属于中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
已知函数y=f(x)(x∈R)是一个以6为最小正周期的奇函数,则f(3)的值为( )
| A、0 | B、6 | C、-6 | D、不能确定 |
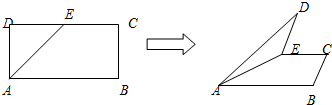
如图,在矩形ABCD中,AB=4,BC=3,E为DC边的中点,沿AE将AD折起,使二面角D-AE-B为60°,则异面直线BC与AD所成的角余弦值为( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f(x)=x2-1在下列定区间上是增函数的是( )
| A、(-∞,0) |
| B、(0,+∞) |
| C、(-∞,1) |
| D、(1,+∞) |
已知△ABC不是直角三角形,三个角∠A、∠B、∠C对应的边分别是a、b、c,记ωA=
•
,ωB=
•
,ωC=
•
,下列结论中,错误的是( )
| AB |
| AC |
| BC |
| BA |
| CA |
| CB |
| A、ωA+ωB=c2 |
| B、ωAωBωC=-(abc)2 |
| C、若ωA=ωB=ωC,则△ABC为等边三角形 |
| D、ωAtanA=ωBtanB=ωCtanC |