题目内容
若A={y|y=2x，x∈R}，B{（x，y）|y=x2，x∈R}，则A∩B的子集个数为（ ）
| A、4 | B、2 | C、1 | D、0 |
考点：交集及其运算
专题：集合
分析：利用指数函数的性质求出A中y的范围确定出A，B为二次函数y=x2上的点集，可得出两集合的交集为空集，即可确定出交集的子集个数．
解答：
解：∵A={y|y=2x，x∈R}，B{（x，y）|y=x2，x∈R}，
∴A∩B=∅，
则A∩B的子集个数为1．
故选：C．
∴A∩B=∅，
则A∩B的子集个数为1．
故选：C．
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
已知函数y=f（x）（x∈R）是一个以6为最小正周期的奇函数，则f（3）的值为（ ）
| A、0 | B、6 | C、-6 | D、不能确定 |
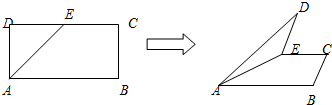
如图，四棱锥P-ABCD中，底面ABCD为平行四边形，∠DAB=60°，AB=2AD，PD⊥底面ABCD．PD=AD如图，在矩形ABCD中，AB=4，BC=3，E为DC边的中点，沿AE将AD折起，使二面角D-AE-B为60°，则异面直线BC与AD所成的角余弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|