题目内容
△A,B,C所对的边分别为a,b,c且2sin2
+cos2C=1
(1)求角C的大小;
(2)若向量
=(3a,b),向量
=(a,-
),
⊥
,(
+
)•(
-
)=16,求a,b,c的值.
| A+B |
| 2 |
(1)求角C的大小;
(2)若向量
| m |
| n |
| b |
| 3 |
| m |
| n |
| m |
| n |
| m |
| n |
考点:二倍角的余弦,平面向量数量积的运算
专题:解三角形
分析:(1)由二倍角公式化简已知式子可得cosC的方程,解方程可得cosC,可得角C的大小;
(2)由已知向量式可得a和b的方程组,解方程组可得a,b,再由由余弦定理可得c值.
(2)由已知向量式可得a和b的方程组,解方程组可得a,b,再由由余弦定理可得c值.
解答:
解:(1)由2sin2
+cos2C=1可得cos2C=1-2sin2
,
∴cos2C=cos(A+B),∴cos2C=-cosC
∴2cos2C-1+cosC=0,解得cosC=
,或cosC=-1(舍去)
∴角C的大小为
;
(2)∵向量
=(3a,b),
=(a,-
),
由
⊥
可得
•
=3a2-
=0,解得b=3a,①
由(
+
)•(
-
)=
2-
2=8a2+
b2=16可得9a2+b2=18,②
联立①②解得a=1且b=3,
由余弦定理可得c=
=
| A+B |
| 2 |
| A+B |
| 2 |
∴cos2C=cos(A+B),∴cos2C=-cosC
∴2cos2C-1+cosC=0,解得cosC=
| 1 |
| 2 |
∴角C的大小为
| π |
| 3 |
(2)∵向量
| m |
| n |
| b |
| 3 |
由
| m |
| n |
| m |
| n |
| b2 |
| 3 |
由(
| m |
| n |
| m |
| n |
| m |
| n |
| 8 |
| 9 |
联立①②解得a=1且b=3,
由余弦定理可得c=
| a2+b2-2abcosC |
| 7 |
点评:本题考查二倍角的余弦公式,涉及余弦定理,属基础题.

练习册系列答案
相关题目
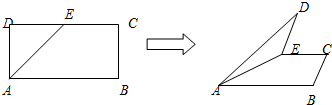
如图,在矩形ABCD中,AB=4,BC=3,E为DC边的中点,沿AE将AD折起,使二面角D-AE-B为60°,则异面直线BC与AD所成的角余弦值为( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列函数存在极值的是( )
A、y=
| ||
| B、y=x-ex | ||
| C、y=x3+x2+2x-3 | ||
| D、y=x3 |
设函数f(x)的定义域为M,若函数f(x)满足条件[m,n]⊆M,使f(x)在[m,n]上的值域是[
,
],则成f(x)为“半缩函数”,若函数f(x)=log3(3x+λ)为“半缩函数”,则λ的范围是( )
| m |
| 2 |
| n |
| 2 |
| A、(0,1) | ||
B、(0,
| ||
C、(0,
| ||
D、(
|
 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.PD=AD
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.PD=AD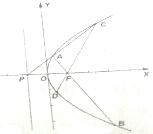 如图,已知F是抛物线y2=4x的焦点,P是抛物线的准线与x轴的交点,过P作直线l交抛物线于不同的两点A、C,点B、D在抛物线上,且
如图,已知F是抛物线y2=4x的焦点,P是抛物线的准线与x轴的交点,过P作直线l交抛物线于不同的两点A、C,点B、D在抛物线上,且