题目内容
设函数f(x)=
-cosx的所有正的极小值点从小到大排成的数列为{xn}.
(1)求数列{xn};
(2)设{xn}的前n项和为Sn,求tanSn.
| π |
| 2 |
(1)求数列{xn};
(2)设{xn}的前n项和为Sn,求tanSn.
考点:数列与三角函数的综合
专题:计算题,作图题,导数的综合应用,等差数列与等比数列,三角函数的图像与性质
分析:(1)作出f(x)=
-cosx的图象,结合图象可得当函数f(x)=
-cosx取得极小值时,cosx=1,从而可得xn=2nπ,n∈N*;
(2)利用等差数列前n项和公式求和,再求正切值.
| π |
| 2 |
| π |
| 2 |
(2)利用等差数列前n项和公式求和,再求正切值.
解答:
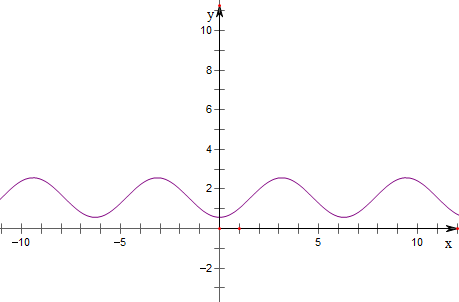 解:(1)f(x)=
解:(1)f(x)=
-cosx的图象如右图,
由图可知,
当函数f(x)=
-cosx取得极小值时,
cosx=1,
即x=2kπ,
故数列{xn}是以2π为首项,2π为公差的等差数列,
即xn=2nπ,n∈N*;
(2)Sn=
n=n(n+1)π;
tanSn=tan(n(n+1)π)=tan0=0.
 解:(1)f(x)=
解:(1)f(x)=| π |
| 2 |
由图可知,
当函数f(x)=
| π |
| 2 |
cosx=1,
即x=2kπ,
故数列{xn}是以2π为首项,2π为公差的等差数列,
即xn=2nπ,n∈N*;
(2)Sn=
| (2π+2nπ) |
| 2 |
tanSn=tan(n(n+1)π)=tan0=0.
点评:本题考查了导数的应用,三角函数的性质与应用,同时考查了数列的通项公式及前n项和,属于中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
若集合A={0,1,2,3,4},集合B={x|x∈A且x-2∉A},则集合B的子集的个数为 ( )
| A、1 | B、2 | C、4 | D、8 |
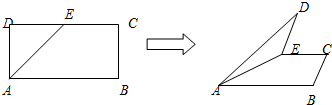
如图,在矩形ABCD中,AB=4,BC=3,E为DC边的中点,沿AE将AD折起,使二面角D-AE-B为60°,则异面直线BC与AD所成的角余弦值为( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列函数存在极值的是( )
A、y=
| ||
| B、y=x-ex | ||
| C、y=x3+x2+2x-3 | ||
| D、y=x3 |
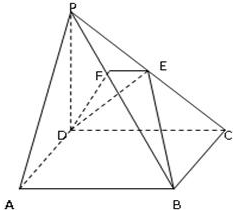 在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ACD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ACD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.