题目内容
3.若$α∈(2kπ+\frac{π}{4},2kπ+\frac{π}{2})$(k∈Z),则sinα,cosα,tanα的大小关系为( )| A. | tanα>sinα>cosα | B. | tanα>cosα>sinα | C. | tanα<sinα<cosα | D. | tanα<cosα<sinα |
分析 利用单位圆中的正切线、正弦线、余弦线,即可得出结论.
解答 解:∵$α∈(2kπ+\frac{π}{4},2kπ+\frac{π}{2})$(k∈Z),
所以在单位圆中,做出角α的正切线、正弦线、余弦线,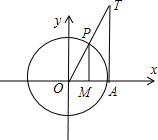
可得正切线最长,余弦线最短,
所以有tanα>sinα>cosα,
故选:A
点评 本题考查利用单位圆中的正切线、正弦线、余弦线的大小来比较对应的三角函数的大小.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
11.若$cos(\frac{π}{6}-α)=m,(|m|≤1)$,则$sin(\frac{2π}{3}-α)$的值为( )
| A. | -m | B. | $-\frac{m}{2}$ | C. | $\frac{m}{2}$ | D. | m |
8.某饮料销售点销售某品牌饮料,饮料的零售价x(元/瓶)与销量y(瓶)的关系统计如下:
由表中数据得线性回归方程:$\widehat{y}$=-20x+a,当零售价为每瓶3.7元时,估计该销售点销售的这种饮料的瓶数为( )
| 零售价x(元/瓶) | 3.0 | 3.2 | 3.4 | 3.6 | 3.8 | 4.0 |
| 销量y(瓶) | 50 | 44 | 43 | 40 | 35 | 28 |
| A. | 39 | B. | 38 | C. | 37 | D. | 36 |
12.极坐标方程ρcosθ=2sin2θ表示的曲线为( )
| A. | 一条射线和一个圆 | B. | 一条直线和一个圆 | ||
| C. | 两条直线 | D. | 一个圆 |
13.已知sinα=$\frac{1}{3}$,则cos(α+$\frac{3π}{2}$)=( )
| A. | $\frac{2\sqrt{2}}{3}$ | B. | -$\frac{2\sqrt{2}}{3}$ | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
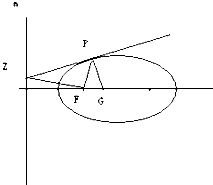 已知:如图,设P为椭圆上的任意一点,过点P作椭圆的切线,交准线m于点Z,此时FZ⊥FP,过点P作PZ的垂线交椭圆的长轴于点G,椭圆的离心率为e,求证:FG=e•FP.
已知:如图,设P为椭圆上的任意一点,过点P作椭圆的切线,交准线m于点Z,此时FZ⊥FP,过点P作PZ的垂线交椭圆的长轴于点G,椭圆的离心率为e,求证:FG=e•FP. 如图,已知PA是⊙O的切线,A是切点,直线PO交⊙O于B、C两点,D是OC的中点,连结AD并延长交⊙O于点E,若PA=2$\sqrt{3}$,∠APB=30°.
如图,已知PA是⊙O的切线,A是切点,直线PO交⊙O于B、C两点,D是OC的中点,连结AD并延长交⊙O于点E,若PA=2$\sqrt{3}$,∠APB=30°.