题目内容
13.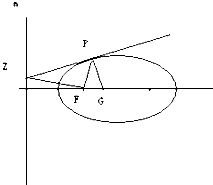 已知:如图,设P为椭圆上的任意一点,过点P作椭圆的切线,交准线m于点Z,此时FZ⊥FP,过点P作PZ的垂线交椭圆的长轴于点G,椭圆的离心率为e,求证:FG=e•FP.
已知:如图,设P为椭圆上的任意一点,过点P作椭圆的切线,交准线m于点Z,此时FZ⊥FP,过点P作PZ的垂线交椭圆的长轴于点G,椭圆的离心率为e,求证:FG=e•FP.
分析 过P作准线的垂线,垂足为N,连接NF,证明△NPF∽△FPG,即可证明FG=e•FP.
解答  证明:过P作准线的垂线,垂足为N,
证明:过P作准线的垂线,垂足为N,
∵FZ⊥FP,
∴P,F,Z,N四点共圆.
连接NF,则∠PNF=∠PZF,
∵PG⊥PZ,
∴∠FPG=∠PZF=∠PNF,
∵PN∥FG,
∴∠NPF=∠PFG,
∴△NPF∽△FPG,
∴$\frac{FG}{FP}=\frac{PF}{PN}$=e,
∴FG=e•FP.
点评 本题考查椭圆的性质,考查三角形相似的证明,正确证明三角形相似是关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
3.函数f(x)=ex(sinx-2)在区间[0,2π]上的最大值是( )
| A. | -2 | B. | -2e2π | C. | -2eπ | D. | -${e}^{\frac{π}{2}}$ |
3.若$α∈(2kπ+\frac{π}{4},2kπ+\frac{π}{2})$(k∈Z),则sinα,cosα,tanα的大小关系为( )
| A. | tanα>sinα>cosα | B. | tanα>cosα>sinα | C. | tanα<sinα<cosα | D. | tanα<cosα<sinα |