题目内容
11.若$cos(\frac{π}{6}-α)=m,(|m|≤1)$,则$sin(\frac{2π}{3}-α)$的值为( )| A. | -m | B. | $-\frac{m}{2}$ | C. | $\frac{m}{2}$ | D. | m |
分析 由条件利用诱导公式化简所给式子的值,可得结果.
解答 解:$sin(\frac{2π}{3}-α)$=sin($\frac{π}{2}$+$\frac{π}{6}$-α)=cos($\frac{π}{6}$-α)=m,
故选:D.
点评 本题主要考查应用诱导公式化简三角函数式,要特别注意符号的选取,这是解题的易错点,属于基础题.

练习册系列答案
相关题目
6.将4个相同的红球和4个相同的蓝球排成一排,从左到右每个球依次对应序号为1,2,…,8,若同颜色的球之间不加区分,则4个红球对应序号之和小于4个蓝球对应序号之和的排列方法种数为( )
| A. | 31 | B. | 27 | C. | 54 | D. | 62 |
3.若$α∈(2kπ+\frac{π}{4},2kπ+\frac{π}{2})$(k∈Z),则sinα,cosα,tanα的大小关系为( )
| A. | tanα>sinα>cosα | B. | tanα>cosα>sinα | C. | tanα<sinα<cosα | D. | tanα<cosα<sinα |
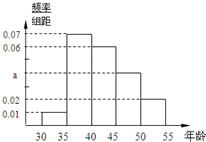 某同学对本地[30,55]岁的爱好阅读的人群随机抽取n人进行了一次调查,得到如下年龄统计表,其中不超过40岁的共有60人.
某同学对本地[30,55]岁的爱好阅读的人群随机抽取n人进行了一次调查,得到如下年龄统计表,其中不超过40岁的共有60人.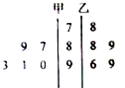 如图是甲、乙两位射击运动员的5次训练成绩(单位:环)的茎叶图,则成绩较为稳定(方差较小)的运动员是甲.
如图是甲、乙两位射击运动员的5次训练成绩(单位:环)的茎叶图,则成绩较为稳定(方差较小)的运动员是甲.