题目内容
12.极坐标方程ρcosθ=2sin2θ表示的曲线为( )| A. | 一条射线和一个圆 | B. | 一条直线和一个圆 | ||
| C. | 两条直线 | D. | 一个圆 |
分析 利用倍角公式,及实数的性质,分解原极坐标方程,再将极坐标方程化为直角坐标方程,就可以得出结论.
解答 解:极坐标方程ρcosθ=2sin2θ可化为:ρcosθ=4sinθcosθ,
∴cosθ=0或ρ=4sinθ,
∴θ=$\frac{π}{2}$或x2+y2-4y=0,
∴极坐标方程ρcosθ=2sin2θ表示的曲线为一条直线和一个圆,
故选:B
点评 研究极坐标问题,我们的解法是将极坐标方程化为直角坐标方程,再进行研究.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.若$α∈(2kπ+\frac{π}{4},2kπ+\frac{π}{2})$(k∈Z),则sinα,cosα,tanα的大小关系为( )
| A. | tanα>sinα>cosα | B. | tanα>cosα>sinα | C. | tanα<sinα<cosα | D. | tanα<cosα<sinα |
17.设m、n为两条不重合的直线,α,β为两个不重合的平面,下列命题中正确的是( )
| A. | 若m、n与α所成的角相等,则m∥n | B. | 若n∥α,m∥β,α∥β,则m∥n | ||
| C. | 若n?α,m?β,m∥n,则α∥β | D. | 若n⊥α,m⊥β,α⊥β,则n⊥m |
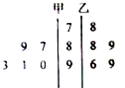 如图是甲、乙两位射击运动员的5次训练成绩(单位:环)的茎叶图,则成绩较为稳定(方差较小)的运动员是甲.
如图是甲、乙两位射击运动员的5次训练成绩(单位:环)的茎叶图,则成绩较为稳定(方差较小)的运动员是甲.