题目内容

15．若正三角形内切圆的半径为r，则该正三角形的周长C（r）=6$\sqrt{3}$r，面积S（r）=3$\sqrt{3}$r2，发现S′（r）=C（r）．相应地，若正四面体内切球的半径为r，则该正四面体的表面积S（r）=24$\sqrt{3}$r2．请用类比推理的方法猜测该正四面体的体积V（r）=8$\sqrt{3}$r3（写出关于r的表达式）．

分析 由题意，V′（r）=S（r），求出原函数，即可得出结论．

解答 解：由题意，V′（r）=S（r），
∵S（r）=24$\sqrt{3}$r2，
∴V′（r）=24$\sqrt{3}$r2．
∴V（r）=8$\sqrt{3}$r3．
故答案为：8$\sqrt{3}$r3．

点评 本题考查类比推理，考查学生的计算能力，比较基础．

练习册系列答案
相关题目
5．（1）已知a，b为实数，并且e＜a＜b，其中e是自然对数的底，证明ab＞ba．
（2）如果正实数a，b满足ab=ba，且a＜1，证明a=b．
6．将4个相同的红球和4个相同的蓝球排成一排，从左到右每个球依次对应序号为1，2，…，8，若同颜色的球之间不加区分，则4个红球对应序号之和小于4个蓝球对应序号之和的排列方法种数为（　　）
A．31B．27C．54D．62
3．若$α∈（2kπ+\frac{π}{4}，2kπ+\frac{π}{2}）$（k∈Z），则sinα，cosα，tanα的大小关系为（　　）
A．tanα＞sinα＞cosαB．tanα＞cosα＞sinαC．tanα＜sinα＜cosαD．tanα＜cosα＜sinα
10．已知函数f（x）=lnx+$\frac{m}{x}$+1（m∈R）．
（Ⅰ）若函数f（x）在[1，e]上的最小值为3．求实数m的值；
（Ⅱ）当m=-1时，判断函数g（x）=f（x）-1+$\frac{lnx}{x}$在其定义域内零点的个数．
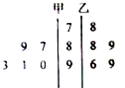20．如图是甲、乙两位射击运动员的5次训练成绩（单位：环）的茎叶图，则成绩较为稳定（方差较小）的运动员是甲．
7．已知函数f（x）=lnx，g（x）=x2．
（Ⅰ）求函数h（x）=f（x）-x+1的最大值；
（Ⅱ）对于任意x1，x2∈（0，+∞），且x1＜x2，是否存在实数m，使mg（x1）-mg（x2）-x2f（x2）+x1f（x1）恒为正数？若存在，求出m的取值范围；若不存在，说明理由．
4．$\overrightarrow{a}$=（2，-1），$\overrightarrow{b}$=（-1，1），则（2$\overrightarrow{a}$+$\overrightarrow{b}$）•$\overrightarrow{a}$=（　　）
A．-5B．7C．5D．-7
5．椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）离心率为$\frac{\sqrt{3}}{2}$，则双曲$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1渐近线方程（　　）
A．x±2y=0B．2x±y=0C．x±4y=0D．x±2y=0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网