题目内容
14.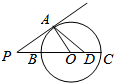 如图,已知PA是⊙O的切线,A是切点,直线PO交⊙O于B、C两点,D是OC的中点,连结AD并延长交⊙O于点E,若PA=2$\sqrt{3}$,∠APB=30°.
如图,已知PA是⊙O的切线,A是切点,直线PO交⊙O于B、C两点,D是OC的中点,连结AD并延长交⊙O于点E,若PA=2$\sqrt{3}$,∠APB=30°.(1)求∠ABO的大小;
(2)求AD的长.
分析 (1)连接AB,求出∠AOB=60°,即可求∠ABO的大小;
(2)过A作AH⊥BC于H,求出HD,即可求AD的长.
解答  解:(1)连接AB,则
解:(1)连接AB,则
∵∠APB=30°,PA是⊙O的切线,A是切点,
∴∠AOB=60°,
∵OA=OB,
∴∠ABO=60°;
(2)过A作AH⊥BC于H,则
∵PA=2$\sqrt{3}$,∠APB=30°,
∴AO=2,AH=$\sqrt{3}$,
Rt△AHD中,HD=2,∴AD=$\sqrt{7}$.
点评 本题考查圆的切线的性质,考查学生的计算能力,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.将4个相同的红球和4个相同的蓝球排成一排,从左到右每个球依次对应序号为1,2,…,8,若同颜色的球之间不加区分,则4个红球对应序号之和小于4个蓝球对应序号之和的排列方法种数为( )
| A. | 31 | B. | 27 | C. | 54 | D. | 62 |
3.若$α∈(2kπ+\frac{π}{4},2kπ+\frac{π}{2})$(k∈Z),则sinα,cosα,tanα的大小关系为( )
| A. | tanα>sinα>cosα | B. | tanα>cosα>sinα | C. | tanα<sinα<cosα | D. | tanα<cosα<sinα |