题目内容
1.若函数y=ax+sinx在R上单调增,则a的最小值为1.分析 该函数在R上单调增,从而导数y′=a+cosx≥0恒成立,即a≥-cosx,从而便可得出a≥1,这便得到a的最小值为1.
解答 解:y′=a+cosx;
∵y=ax+sinx在R上单调增;
∴a+cosx≥0;
∴a≥-cosx;
-cosx的最大值为1;
∴a≥1;
即a的最小值为1.
故答案为:1.
点评 考查增函数的定义,函数的单调性和函数导数符号的关系,以及余弦函数的最值.

练习册系列答案
相关题目
10.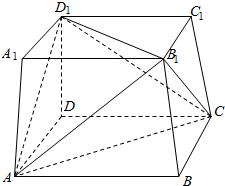 在正方体ABCD-A1B1C1D1中,三棱锥D1-AB1C的表面积与正方体的表面积的比为( )
在正方体ABCD-A1B1C1D1中,三棱锥D1-AB1C的表面积与正方体的表面积的比为( )
 在正方体ABCD-A1B1C1D1中,三棱锥D1-AB1C的表面积与正方体的表面积的比为( )
在正方体ABCD-A1B1C1D1中,三棱锥D1-AB1C的表面积与正方体的表面积的比为( )| A. | 1:1 | B. | 1;$\sqrt{2}$ | C. | 1:$\sqrt{3}$ | D. | 1;2 |
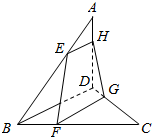 如图所示,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD,DA上的点.且满足$\frac{AE}{EB}$=$\frac{AH}{HD}$=$\frac{1}{2}$,$\frac{CF}{FB}$=$\frac{CG}{GD}$=2.
如图所示,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD,DA上的点.且满足$\frac{AE}{EB}$=$\frac{AH}{HD}$=$\frac{1}{2}$,$\frac{CF}{FB}$=$\frac{CG}{GD}$=2.