题目内容
12.设不等式组$\left\{\begin{array}{l}{x+y≤2}\\{2x-y≤1}\\{x≥0,y≥0}\end{array}\right.$表示的平面区域为D,向区域D内任投一点P,则点P落在圆x2+y2=2内的概率为$\frac{5}{π+1}$.分析 首先分别画出区域D、M,然后分别计算面积,利用几何概型的公式解答即可.
解答  解:平面区域D以及满足条件的P如图阴影部分
解:平面区域D以及满足条件的P如图阴影部分
区域D的面积为$\frac{1}{2}×1×1+\frac{1}{2}×(\frac{1}{2}+1)×1$=$\frac{5}{4}$,
落在圆x2+y2=2内的区域M的面积为$\frac{2π}{8}$+$\frac{1}{2}×\frac{1}{2}×1$=$\frac{π+1}{4}$,
由几何概型的公式得点P落在圆x2+y2=2内的概率为$\frac{5}{π+1}$.
故答案为:$\frac{5}{π+1}$.
点评 本题考查了几何概型的概率公式的运用;关键是明确区域的面积,利用公式解答.

练习册系列答案
相关题目
2.等轴双曲线C的中心在原点,右焦点与抛物线${y^2}=8\sqrt{2}x$的焦点重合,则C的实轴长为( )
| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 4 | D. | 8 |
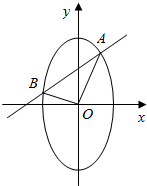 已知椭圆C的方程为x2+$\frac{{y}^{2}}{4}$=1,定点N(0,1),过圆M:x2+y2=$\frac{4}{5}$上任意一点作圆M的一条切线交椭圆C于A、B两点.
已知椭圆C的方程为x2+$\frac{{y}^{2}}{4}$=1,定点N(0,1),过圆M:x2+y2=$\frac{4}{5}$上任意一点作圆M的一条切线交椭圆C于A、B两点.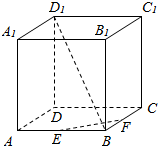 在正方体ABCD-A1B1C1D1中,E、F分别是AB,BC的中点,求异面直线BD1、EF所成角的大小.
在正方体ABCD-A1B1C1D1中,E、F分别是AB,BC的中点,求异面直线BD1、EF所成角的大小.