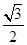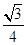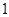题目内容
用一个平面去截正方体,对于截面的边界,有以下图形:
①钝角三角形;②直角梯形;③菱形;④正五边形;⑤正六边形。
则不可能的图形的选项为( )
| A.③④⑤ | B.①②⑤ | C.①②④ | D.②③④ |
C
解析试题分析:用一个平面去截正方体,对于截面的边界①三角形只能是直角三角形和锐角三角形
②不会是直角梯形,而是等腰梯形,或者一般梯形;③菱形,可以对称的平行截面饿到。
④正五边形不能得到。⑤正六边形,过各个面的底边的中点得到,成立,故选C.
考点:截面问题
点评:解决的关键是通过不同角度的作出截面来得到分析,属于基础题。

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
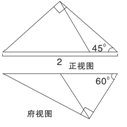
一个三棱锥的三视图如图,则该三棱锥的体积为( )
A. | B. | C. | D. |
一平面截一球得到直径是6cm的圆面,球心到这个平面的距离是4cm,则该球的体积
A. | B. | C.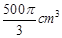 | D. |
已知A,B,C,D是同一球面上的四个点,其中△ABC是正三角形,AD⊥平面ABC,AD=2AB=6则该球的表面积为
A.16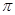 | B.24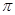 | C.32 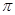 | D.48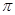 |
长方体一个顶点上三条棱的长分别为3、4、5,且它的八个顶点都在同一球面上,这个球的表面积是( )
A.20 π π | B.25 π π | C.50π | D.200π |
已知某几何体的三视图如图所示,若该几何体的体积为24,则正视图中a的值为
| A.8 | B.6 |
| C.4 | D.2 |
一个几何体的三视图如右图所示,则它的体积为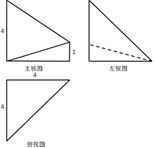
A.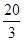 | B.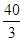 |
C.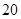 | D.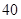 |
如图在棱长为5的正方体 中,
中, 是棱
是棱 上的一条线段,且
上的一条线段,且 ,
, 是
是 中点,点
中点,点 是棱
是棱 上动点,则四面体
上动点,则四面体 的体积( )
的体积( )
| A.是变量且有最大值 | B.是变量且有最小值 |
| C.是变量且有最大值和最小值 | D.是常量 |