题目内容
已知A,B,C,D是同一球面上的四个点,其中△ABC是正三角形,AD⊥平面ABC,AD=2AB=6则该球的表面积为
A.16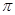 | B.24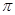 | C.32 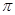 | D.48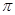 |
C
解析试题分析:
由题意画出几何体的图形如图:
把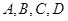 扩展为三棱锥,
扩展为三棱锥,
上下地面中心连线的中点与A的距离为球的半径,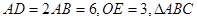 是正三角形,
是正三角形,
所以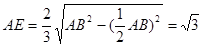 ,
, 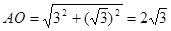
所以球的体积为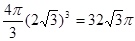 .
.
考点:球的体积和表面积 棱锥的结构特征 球内接多面体
点评:本题考查球的内接体与球的关系,考查空间想象能力,利用割补法结合球内接多面体的几何特征求出的半径是解题的关键.

练习册系列答案
相关题目
已知平面 截一球面得圆M,过圆心M且与
截一球面得圆M,过圆心M且与 成
成 角的平面
角的平面 截该球面得圆N若圆M、圆N面积分别为4
截该球面得圆N若圆M、圆N面积分别为4 、13
、13 ,则球面面积为
,则球面面积为
A.36 | B.48 | C.64 | D.100 |
一个棱锥的三视图如图(尺寸的长度单位为 ),则该棱锥的体积是
),则该棱锥的体积是 
A. | B.8 | C.4 | D. |
某几何体的三视图如图所示,其中三角形的三边长与圆的直径均为2,则该几何体的体积为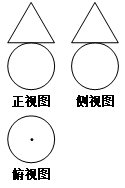
A.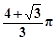 | B.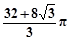 |
C.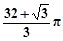 | D.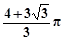 |
用一个平面去截正方体,对于截面的边界,有以下图形:
①钝角三角形;②直角梯形;③菱形;④正五边形;⑤正六边形。
则不可能的图形的选项为( )
| A.③④⑤ | B.①②⑤ | C.①②④ | D.②③④ |
已知几何体M的正视图是一个面积为2 的半圆,俯视图是正三角形,那么这个几何体的表面积和体积为
的半圆,俯视图是正三角形,那么这个几何体的表面积和体积为
A.6 和 和  | B.6 +4 +4 和 和  |
C.6 +4 +4 和 和  | D.4( + + )和 )和  |
一个棱锥的三视图如图,则该棱锥的全面积(单位: )为
)为
A. | B. |
C. | D. |
 的棱长为1,动点
的棱长为1,动点 在此正方体的表面上运动,且
在此正方体的表面上运动,且 ,记点
,记点 ,则函数
,则函数


 B.
B.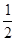 C. 1 D.
C. 1 D.