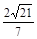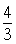题目内容
一个三棱锥的三视图如图,则该三棱锥的体积为( )
A. | B. | C. | D. |
A
解析试题分析:有三视图可知该几何体(三棱锥)底面是直角三角形,两直角边长为1,2棱锥高为1,所以体积为
考点:三视图及几何体体积
点评:先由三视图的特征结合基本几何体的特点推测出几何体的形状,再带入相应的公式计算

练习册系列答案
相关题目
已知平面 截一球面得圆M,过圆心M且与
截一球面得圆M,过圆心M且与 成
成 角的平面
角的平面 截该球面得圆N若圆M、圆N面积分别为4
截该球面得圆N若圆M、圆N面积分别为4 、13
、13 ,则球面面积为
,则球面面积为
A.36 | B.48 | C.64 | D.100 |
某几何体的三视图如图所示,则它的体积是
A. | B. | C.8-2π | D. |
一个棱锥的三视图如图(尺寸的长度单位为 ),则该棱锥的体积是
),则该棱锥的体积是 
A. | B.8 | C.4 | D. |
用一个平面去截正方体,对于截面的边界,有以下图形:
①钝角三角形;②直角梯形;③菱形;④正五边形;⑤正六边形。
则不可能的图形的选项为( )
| A.③④⑤ | B.①②⑤ | C.①②④ | D.②③④ |




 ,求其直径
,求其直径 的一个近似公式
的一个近似公式 . 人们还用过一些类似的近似公式. 根据
. 人们还用过一些类似的近似公式. 根据 判断,下列近似公式中最精确的一个是( )
判断,下列近似公式中最精确的一个是( )

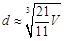
 三点,其中点
三点,其中点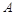 与
与 两点间的球面距离均为
两点间的球面距离均为 ,
, ,则球心到平面
,则球心到平面 的距离为( )
的距离为( )