题目内容
已知某几何体的三视图如图所示,若该几何体的体积为24,则正视图中a的值为
| A.8 | B.6 |
| C.4 | D.2 |
B
解析试题分析:解:由三视图知几何体是一个四棱锥,底面是一个边长分别是a和3的矩形,一条侧棱与底面垂直,且这条侧棱的长是4,根据该几何体的体积是24,得到 ∴a=6,故选B
∴a=6,故选B
考点:由三视图求几何体的体积
点评:本题考查由三视图求几何体的体积,实际上不是求几何体的体积,而是根据体积的值和体积的计算公式,写出关于变量的方程,利用方程思想解决问题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
用一个平面去截正方体,对于截面的边界,有以下图形:
①钝角三角形;②直角梯形;③菱形;④正五边形;⑤正六边形。
则不可能的图形的选项为( )
| A.③④⑤ | B.①②⑤ | C.①②④ | D.②③④ |
一个几何体的三视图如右图所示,且其左视图是一个等边三角形,则这个几何体的体积为( )
A. | B. |
C. | D.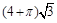 |
已知几何体M的正视图是一个面积为2 的半圆,俯视图是正三角形,那么这个几何体的表面积和体积为
的半圆,俯视图是正三角形,那么这个几何体的表面积和体积为
A.6 和 和  | B.6 +4 +4 和 和  |
C.6 +4 +4 和 和  | D.4( + + )和 )和  |
如果一个几何体的三视图如图所示,则该几何体的表面积为( )
A.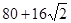 | B. | C.96 | D.80 |
一简单组合体的三视图及尺寸如图示(单位: )则该组合体的体积为.
)则该组合体的体积为.


A.72000 | B.64000 |
C.56000 | D.44000 |
在长方体ABCD—A1B1C1D1中,有( )条棱所在的直线与直线AA1是异面直线且互相垂直。
| A.2 | B.4 | C.6 | D.8 |



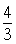


 B.
B.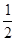 C. 1 D.
C. 1 D.