题目内容
【题目】在数列{an}中,a3=12,a11=﹣5,且任意连续三项的和均为11,则a2017=;设Sn是数列{an}的前n项和,则使得Sn≤100成立的最大整数n= .
【答案】4;29
【解析】解:由题意可得an+an+1+an+2=11,
将n换为an+1+an+2+an+3=11,
可得an+3=an,
可得数列{an}是周期为3的数列.
a3=12,a11=﹣5,即有a2=﹣5,a1=11﹣12+5=4,
可得a2017=a3×672+1=a1=4;
当n=3k,k为自然数,时,Sn=11k;
当n=3k+1,k为自然数时,Sn=11k+4;
当n=3k+2,k为自然数时,Sn=11k+4﹣5=11k﹣1;
使得Sn≤100成立,
由11k≤100,可得k的最大值为9,此时n=27;
由11k+4≤100,可得k的最大值为8,此时n=25;
由11k﹣1≤100,可得k的最大值为9,此时n=29.
则使得Sn≤100成立的最大整数n为29.
所以答案是:4,29.
【考点精析】掌握数列的前n项和是解答本题的根本,需要知道数列{an}的前n项和sn与通项an的关系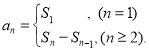 .
.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目