题目内容
【题目】已知 ![]() 且满足不等式
且满足不等式 ![]() .
.
(1)求不等式 ![]() ;
;
(2)若函数 ![]() 在区间
在区间 ![]() 有最小值为
有最小值为 ![]() ,求实数
,求实数 ![]() 值.
值.
【答案】
(1)解:∵22a+1>25a-2.
∴2a+1>5a-2,即3a<3
∴a<1,
∵a>0,a<1
∴0<a<1.
∵loga(3x+1)<loga(7-5x).
∴等价为 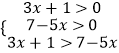 , 即
, 即 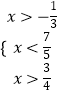 , ∴
, ∴ ![]() ,
,
即不等式的解集为( ![]() ,
, ![]() )
)
(2)解:∵0<a<1
∴函数y=loga(2x-1)在区间[3,6]上为减函数,
∴当x=6时,y有最小值为-2, 即loga11=-2,
∴a-2= ![]() =11, 解得a=
=11, 解得a= ![]()
【解析】(1)先求出a的取值范围,再根据对数函数的图象和性质,可得函数单调递减且3x+1>0,75x>0,3x+1>75x同时成立,解方程组即可得到x的范围。
(2)根据对数函数的单调性和最值,可知在x=6时取得最小值-2,代入再进行指对互换,即可求得a的值。

练习册系列答案
相关题目
【题目】从某企业生产的某种产品中抽取100件样本,测量这些样本的一项质量指标值,由测量结果得如下频数分布表:
质量指标 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125] |
频数 | 6 | 26 | 38 | 22 | 8 |
则样本的该项质量指标值落在[105,125]上的频率为 .