Question

【题目】已知正方体ABCD﹣A1B1C1D1 ， 则AC与平面BDC1所成角的余弦值为（ ）
A.
B.
C.
D.

Answer 1

【答案】B
【解析】解：以A1为原点建立如图所示的空间直角坐标系，
∵A1A⊥平面ABCD，∴A1A⊥BD，
又BD⊥AC，A1A与AC为平面A1AC内的相交直线，
∴BD⊥平面A1AC，
∴BD⊥A1C，
同理可证：BC1⊥A1C，
∴A1C⊥平面BDC1 ， ∴ 是平面BDC1的一个法向量，
设正方体棱长为1，
则 =（1，1，1）， =（1，1，0）， =2，| |= ，| |= ，
∴cos＜ ， ＞= = ，
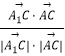设AC与平面BDC1所成角为α，则sinα= ，∴cosα= ．
故选：B．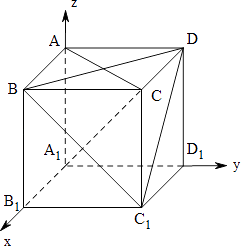

【考点精析】本题主要考查了空间角的异面直线所成的角的相关知识点，需要掌握已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则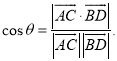才能正确解答此题．