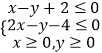题目内容
【题目】如图所示，已知P（4，0）是圆x2+y2=36内的一点，A、B是圆上两动点，且满足∠APB=90°，求矩形APBQ的顶点Q的轨迹方程．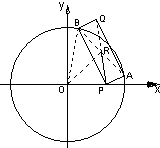 
【答案】解：设AB的中点为R，则R也是PQ的中点，设R的坐标为（x1 ， y1），则在Rt△ABP中，|AR|=|PR|．
又因为R是弦AB的中点，依垂径定理：在Rt△OAR中，|AR|2=|AO|2﹣|OR|2=36﹣（ 
）．
又|AR|=|PR|= 
，所以有（x1﹣4）2+ 
=36﹣（ ），即 ﹣4x1﹣10=0．
因此点R在一个圆上，而当R在此圆上运动时，Q点即在所求的轨迹上运动．
设Q（x，y），因为R是PQ的中点，所以x1= 
，
代入方程 ﹣4x1﹣10=0，得 
﹣10=0，
整理得：x2+y2=56，这就是所求的Q点的轨迹方程．
【解析】设AB的中点为R，设R的坐标为（x1 ， y1），则在Rt△ABP中，|AR|=|PR|，在Rt△OAR中，|AR|2=|AO|2﹣|OR|2=36﹣（ 
），再由|AR|=|PR|= 
，由此得到点R的轨迹方程 ﹣4x1﹣10=0①，设Q（x，y），因为R是PQ的中点，可得x1= 
，代入①化简即得所求．
练习册系列答案
相关题目
