Question

【题目】设二次函数，关于的不等式的解集有且只有一个元素．

（1）设数列的前项和，求数列的通项公式；

（2）记，则数列中是否存在不同的三项成等比数列？若存在，求出这三项，若不存在，请说明理由．

Answer 1

【答案】（1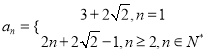）；（2）不存在不同的三项能组成等比数列．

【解析】试题分析：（1）因为关于的不等式的解集有且只有一个元素，所以二次函数的图象与轴相切，则，得，所以数列的前项和由与的关系求（2），假设数列中存在三项成等比数列，则，即，整理得，因为都是正整数，所以，整理得与题意矛盾.

试题解析：

（1）因为关于的不等式的解集有且只有一个元素，

所以二次函数的图象与轴相切，

则，考虑到，所以，

从而，

所以数列的前项和，

于是当时， ，

当时， ，不适合上式，

所以数列的通项公式为；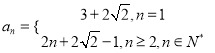

（2）．

假设数列中存在三项成等比数列，则，

即，整理得，

因为都是正整数，所以，

于是，即，从而，与矛盾，

故数列中不存在不同的三项能组成等比数列．