题目内容
.设集合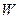 是满足下列两个条件的无穷数列
是满足下列两个条件的无穷数列 的集合:
的集合:
①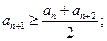 ②
②
 是与
是与 无关的常数.
无关的常数.
(Ⅰ)若 是等差数列,
是等差数列, 是其前n项的和,
是其前n项的和, ,证明:
,证明: ;
;
(Ⅱ)设数列 的通项为
的通项为 ,求
,求 的取值范围;
的取值范围;
(Ⅲ)设数列 的各项均为正整数,且
的各项均为正整数,且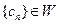 ,试证
,试证 .
.
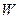 是满足下列两个条件的无穷数列
是满足下列两个条件的无穷数列 的集合:
的集合:①
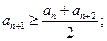 ②
②
 是与
是与 无关的常数.
无关的常数.(Ⅰ)若
 是等差数列,
是等差数列, 是其前n项的和,
是其前n项的和, ,证明:
,证明: ;
;(Ⅱ)设数列
 的通项为
的通项为 ,求
,求 的取值范围;
的取值范围;(Ⅲ)设数列
 的各项均为正整数,且
的各项均为正整数,且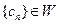 ,试证
,试证 .
.(Ⅰ)同解析(Ⅱ) ≥7(Ⅲ)同解析
≥7(Ⅲ)同解析
 ≥7(Ⅲ)同解析
≥7(Ⅲ)同解析(Ⅰ)设等差数列{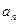 }的公差是
}的公差是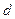 ,则
,则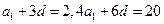 ,解得
,解得 所以
所以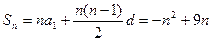 ……………………3分
……………………3分
由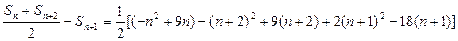 =-1<0
=-1<0
得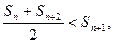 适合条件①;……………………5分
适合条件①;……………………5分
又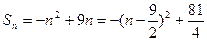 ,所以当
,所以当 =4或5时,
=4或5时, 取得最大值20,即
取得最大值20,即 ≤20,适合条件②.综上所述,
≤20,适合条件②.综上所述, 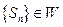 ……………………7分
……………………7分
(Ⅱ)因为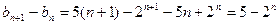 ,所以当n≥3时,
,所以当n≥3时,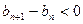 ,此时数列
,此时数列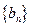 单调递减;当
单调递减;当 =1,2时,
=1,2时,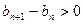 ,即
,即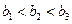
因此数列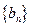 中的最大项是
中的最大项是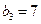 ,所以
,所以 ≥7 ……………………12分
≥7 ……………………12分
(Ⅲ)假设存在正整数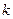 ,使得
,使得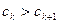 成立,
成立,
由数列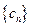 的各项均为正整数,可得
的各项均为正整数,可得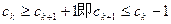
因为 ………14分
………14分
由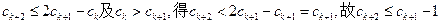
因为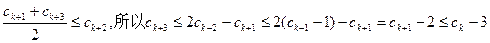
依次类推,可得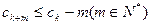 ……………………17分
……………………17分
又存在 ,使
,使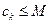 ,总有
,总有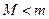 ,故有
,故有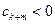 ,这与数列(
,这与数列(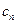 )的各项均为正整数矛盾!
)的各项均为正整数矛盾!
所以假设不成立,即对于任意 ,都有
,都有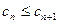 成立.………………18分
成立.………………18分
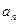 }的公差是
}的公差是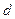 ,则
,则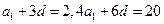 ,解得
,解得 所以
所以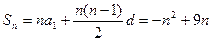 ……………………3分
……………………3分由
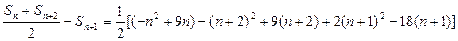 =-1<0
=-1<0得
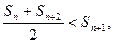 适合条件①;……………………5分
适合条件①;……………………5分又
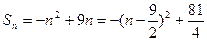 ,所以当
,所以当 =4或5时,
=4或5时, 取得最大值20,即
取得最大值20,即 ≤20,适合条件②.综上所述,
≤20,适合条件②.综上所述, 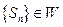 ……………………7分
……………………7分(Ⅱ)因为
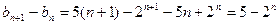 ,所以当n≥3时,
,所以当n≥3时,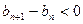 ,此时数列
,此时数列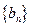 单调递减;当
单调递减;当 =1,2时,
=1,2时,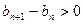 ,即
,即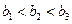
因此数列
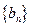 中的最大项是
中的最大项是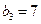 ,所以
,所以 ≥7 ……………………12分
≥7 ……………………12分(Ⅲ)假设存在正整数
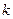 ,使得
,使得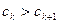 成立,
成立,由数列
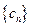 的各项均为正整数,可得
的各项均为正整数,可得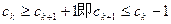
因为
 ………14分
………14分由
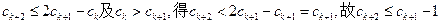
因为
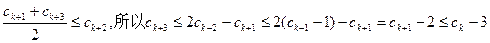
依次类推,可得
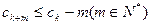 ……………………17分
……………………17分又存在
 ,使
,使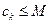 ,总有
,总有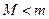 ,故有
,故有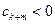 ,这与数列(
,这与数列(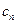 )的各项均为正整数矛盾!
)的各项均为正整数矛盾!所以假设不成立,即对于任意
 ,都有
,都有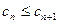 成立.………………18分
成立.………………18分
练习册系列答案
相关题目
 满足:
满足: ,且
,且
 .
. 的值;
的值; ;
; ,求证:
,求证: .
.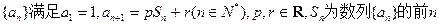 项和.
项和.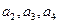 的值
的值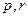 ,使得数列{
,使得数列{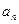 }为等比数列?若存在,求出p,r满足的条件;若不存在,说明理由.
}为等比数列?若存在,求出p,r满足的条件;若不存在,说明理由. 满足:
满足: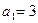 ,且
,且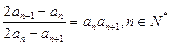 .
.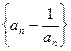 是等比数列;
是等比数列;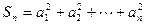 ,
,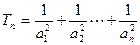 ,求
,求 ,并确定最小的正整数n,使
,并确定最小的正整数n,使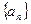 中,
中,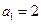 ,
,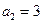 ,其前
,其前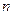 项和
项和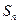 满足
满足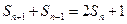 其中(
其中(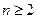 ,
,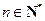 ).
).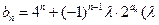 为非零整数,
为非零整数,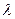 的值,使得对任意
的值,使得对任意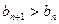 成立.
成立.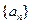 的前
的前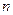 项和为
项和为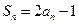 ,数列
,数列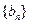 满足
满足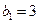 ,
,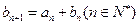 .
.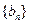 的通项公式; (2)求数列
的通项公式; (2)求数列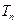 ;
;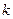 ,使得数列
,使得数列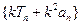 为等差数列,证明你的结论.
为等差数列,证明你的结论.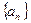 的公差
的公差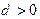 ,满足
,满足 ,
,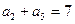 ,设
,设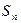 ,则
,则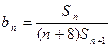 的最大值为
的最大值为 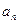 }的通项公式为
}的通项公式为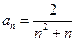 ,那么
,那么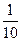 是它的( )
是它的( ) 的前n项和为
的前n项和为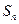 ,若
,若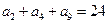 ,则
,则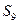 = ;
= ;