题目内容
(本小题满分16分)已知数列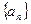 中,
中,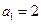 ,
,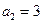 ,其前
,其前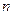 项和
项和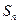 满足
满足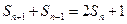 其中(
其中(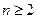 ,
,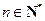 ).
).
(1)求数列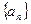 的通项公式;
的通项公式;
(2)设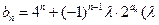 为非零整数,
为非零整数,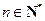 ),试确定
),试确定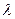 的值,使得对任意
的值,使得对任意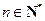 ,都有
,都有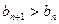 成立.
成立.
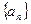 中,
中,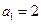 ,
,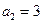 ,其前
,其前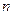 项和
项和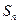 满足
满足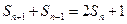 其中(
其中(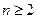 ,
,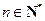 ).
).(1)求数列
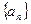 的通项公式;
的通项公式;(2)设
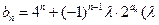 为非零整数,
为非零整数,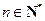 ),试确定
),试确定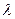 的值,使得对任意
的值,使得对任意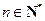 ,都有
,都有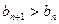 成立.
成立. (1)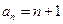 .(2)存在
.(2)存在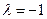 ,使得对任意
,使得对任意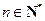 ,都有
,都有
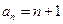 .(2)存在
.(2)存在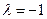 ,使得对任意
,使得对任意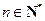 ,都有
,都有
(1)由已知,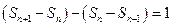 (
(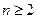 ,
,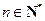 ),
),
即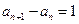 (
(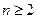 ,
,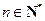 ),且
),且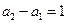 .
.
∴数列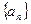 是以
是以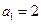 为首项,公差为1的等差数列. ∴
为首项,公差为1的等差数列. ∴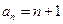 .
.
(2)∵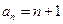 ,∴
,∴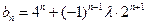 ,要使
,要使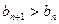 恒成立,
恒成立,
∴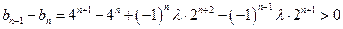 恒成立,
恒成立,
∴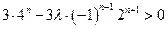 恒成立, ∴
恒成立, ∴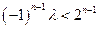 恒成立.
恒成立.
(ⅰ)当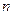 为奇数时,即
为奇数时,即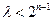 恒成立,
恒成立,
当且仅当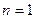 时,
时,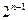 有最小值为1, ∴
有最小值为1, ∴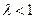 .
.
(ⅱ)当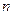 为偶数时,即
为偶数时,即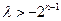 恒成立,
恒成立,
当且仅当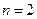 时,
时,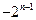 有最大值
有最大值 , ∴
, ∴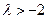 .
.
即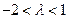 ,又
,又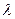 为非零整数,则
为非零整数,则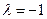 .
.
综上所述,存在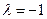 ,使得对任意
,使得对任意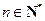 ,都有
,都有 .
.
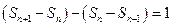 (
(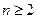 ,
,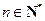 ),
), 即
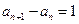 (
(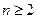 ,
,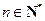 ),且
),且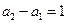 .
.∴数列
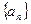 是以
是以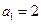 为首项,公差为1的等差数列. ∴
为首项,公差为1的等差数列. ∴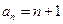 .
.(2)∵
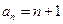 ,∴
,∴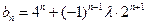 ,要使
,要使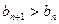 恒成立,
恒成立,∴
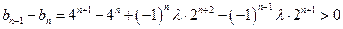 恒成立,
恒成立,∴
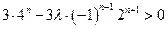 恒成立, ∴
恒成立, ∴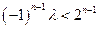 恒成立.
恒成立. (ⅰ)当
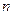 为奇数时,即
为奇数时,即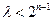 恒成立,
恒成立,当且仅当
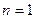 时,
时,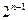 有最小值为1, ∴
有最小值为1, ∴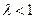 .
. (ⅱ)当
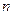 为偶数时,即
为偶数时,即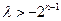 恒成立,
恒成立,当且仅当
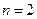 时,
时,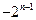 有最大值
有最大值 , ∴
, ∴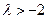 .
. 即
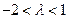 ,又
,又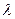 为非零整数,则
为非零整数,则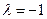 .
.综上所述,存在
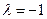 ,使得对任意
,使得对任意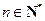 ,都有
,都有 .
.
练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
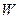 是满足下列两个条件的无穷数列
是满足下列两个条件的无穷数列 的集合:
的集合: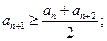 ②
②
 是与
是与 无关的常数.
无关的常数. 是其前n项的和,
是其前n项的和, ,证明:
,证明: ;
; 的通项为
的通项为 ,求
,求 的各项均为正整数,且
的各项均为正整数,且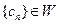 ,试证
,试证 .
.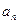 }满足
}满足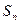 =
=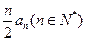 ,
,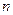 项的和,
项的和,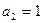 . (1)求
. (1)求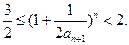
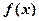 ,存在实数
,存在实数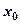 ,使得对于任意实数
,使得对于任意实数 ,总有
,总有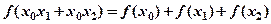 恒成立。
恒成立。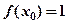 ,且对任意
,且对任意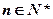 ,有
,有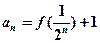 ,求{an}的通项公式;
,求{an}的通项公式;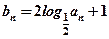 ,将数列{bn}的项重新组合成新数列
,将数列{bn}的项重新组合成新数列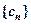 ,具体法则如下:
,具体法则如下: ,……,求证:
,……,求证: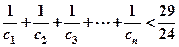 。
。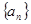 中,
中,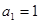 ,
,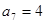 ,数列
,数列 为等比数列,
为等比数列,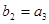 ,
,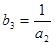 ,则满足
,则满足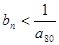 的最小正整数
的最小正整数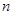 是( )
是( )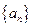 是等差数列,
是等差数列,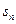 是前n项和,且
是前n项和,且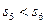 ,
,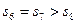 ,则下列结论错误的是
,则下列结论错误的是


 和
和 均为
均为
 ,1,0,…推测出每项公式
,1,0,…推测出每项公式
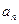 }的前
}的前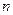 项和
项和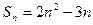 ,第
,第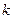 项满足
项满足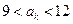 ,则
,则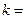 ( )
( )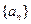 中,
中,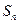 是其前
是其前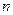 项和,若
项和,若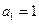 ,
,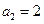 ,
,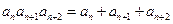 ,
,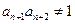 ,则
,则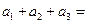 _______________,
_______________,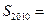 _______________.
_______________.