题目内容
若数列
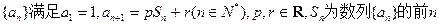 项和.
项和.(I)当p=2,r=0时,求
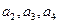 的值
的值(II)是否存在实数
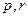 ,使得数列{
,使得数列{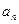 }为等比数列?若存在,求出p,r满足的条件;若不存在,说明理由.
}为等比数列?若存在,求出p,r满足的条件;若不存在,说明理由.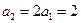 ,
, 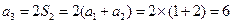 ,
, 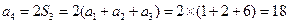
当
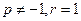 时,数列
时,数列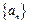 为等比数列.
为等比数列.解:(I)因为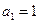 ,
, ,当
,当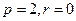 时,
时,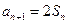
所以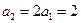 ,
,
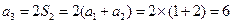 ,
,
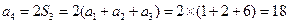 .
.
(II)因为 ,所以
,所以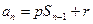 (
(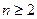 )
)
所以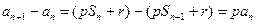
即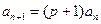 ,其中
,其中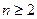
所以若数列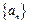 为等比数列,则公比
为等比数列,则公比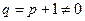 ,所以
,所以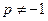 ,
,
又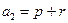 =
= ,故
,故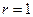
所以当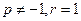 时,数列
时,数列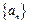 为等比数列.
为等比数列.
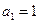 ,
, ,当
,当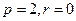 时,
时,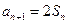
所以
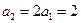 ,
, 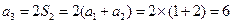 ,
, 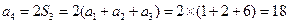 .
. (II)因为
 ,所以
,所以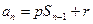 (
(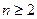 )
)所以
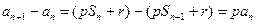
即
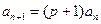 ,其中
,其中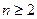
所以若数列
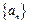 为等比数列,则公比
为等比数列,则公比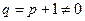 ,所以
,所以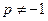 ,
,又
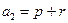 =
= ,故
,故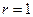
所以当
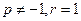 时,数列
时,数列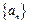 为等比数列.
为等比数列. 
练习册系列答案
相关题目
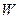 是满足下列两个条件的无穷数列
是满足下列两个条件的无穷数列 的集合:
的集合: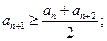 ②
②
 是与
是与 无关的常数.
无关的常数. 是其前n项的和,
是其前n项的和, ,证明:
,证明: ;
; 的通项为
的通项为 ,求
,求 的各项均为正整数,且
的各项均为正整数,且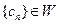 ,试证
,试证 .
.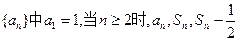 成等比数列。
成等比数列。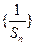 是等差数列;
是等差数列;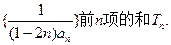
 为等差数列
为等差数列 的前n项和,
的前n项和, ,
,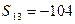 ,则
,则 与
与 的等比中项为( )
的等比中项为( )



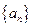 是等差数列,
是等差数列,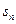 是前n项和,且
是前n项和,且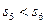 ,
,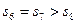 ,则下列结论错误的是
,则下列结论错误的是


 和
和 均为
均为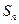 是等差数列
是等差数列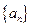 的前
的前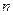 项和,若
项和,若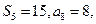 则
则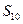 的值为( )
的值为( )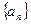 为等差数列,且
为等差数列,且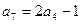 ,
,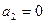 ,则公差d="( "
,则公差d="( "  )
)


 的前
的前 项和为
项和为 ,若
,若 则
则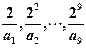 中最大的( )
中最大的( ) .
.
 .
.
 .
.
 .
.