题目内容
(本小题满分13分)已知数列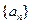 的前
的前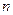 项和为
项和为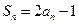 ,数列
,数列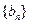 满足
满足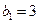 ,
,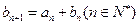 .
.
(1)求数列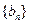 的通项公式; (2)求数列
的通项公式; (2)求数列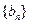 的前
的前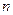 项和
项和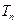 ;
;
(3)是否存在非零实数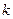 ,使得数列
,使得数列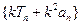 为等差数列,证明你的结论.
为等差数列,证明你的结论.
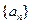 的前
的前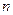 项和为
项和为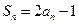 ,数列
,数列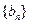 满足
满足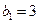 ,
,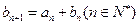 .
.(1)求数列
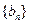 的通项公式; (2)求数列
的通项公式; (2)求数列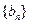 的前
的前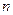 项和
项和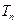 ;
;(3)是否存在非零实数
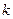 ,使得数列
,使得数列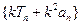 为等差数列,证明你的结论.
为等差数列,证明你的结论.(1)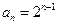 (2)
(2)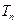
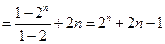 (3)
(3)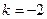 ,使得数列
,使得数列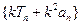 为首项为
为首项为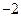 ,公差为
,公差为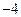 的等差数列
的等差数列
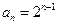 (2)
(2)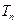
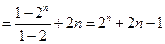 (3)
(3)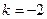 ,使得数列
,使得数列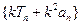 为首项为
为首项为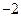 ,公差为
,公差为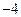 的等差数列
的等差数列(1)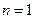 ,
,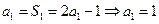
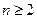 时,
时,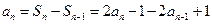 …………………2分
…………………2分
∴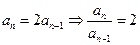 …………………3分
…………………3分
∴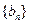 是以1为首项,2为公比的等比数列. ∴
是以1为首项,2为公比的等比数列. ∴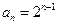 …………………4分
…………………4分
(2)∵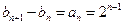
∴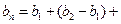 …
…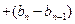 …………………5分
…………………5分
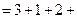 …
…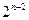 ……………………6分
……………………6分
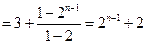 ……………………7分
……………………7分
∴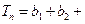 …
…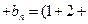 …
…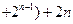
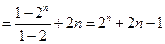 ……9分
……9分
(3)设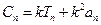
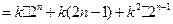
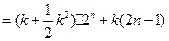 ……………11分
……………11分
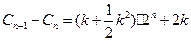 与
与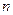 无关 ………………………12分
无关 ………………………12分
∴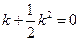 ∵
∵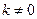
∴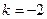 ,使得数列
,使得数列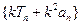 为首项为
为首项为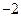 ,公差为
,公差为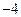 的等差数列. ……13分
的等差数列. ……13分
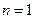 ,
,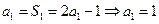
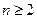 时,
时,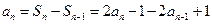 …………………2分
…………………2分∴
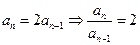 …………………3分
…………………3分∴
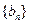 是以1为首项,2为公比的等比数列. ∴
是以1为首项,2为公比的等比数列. ∴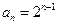 …………………4分
…………………4分(2)∵
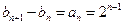
∴
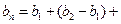 …
…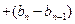 …………………5分
…………………5分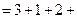 …
…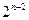 ……………………6分
……………………6分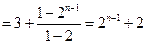 ……………………7分
……………………7分∴
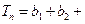 …
…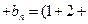 …
…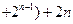
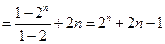 ……9分
……9分(3)设
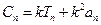
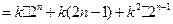
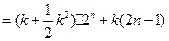 ……………11分
……………11分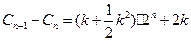 与
与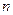 无关 ………………………12分
无关 ………………………12分∴
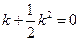 ∵
∵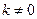
∴
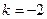 ,使得数列
,使得数列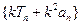 为首项为
为首项为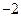 ,公差为
,公差为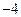 的等差数列. ……13分
的等差数列. ……13分
练习册系列答案
相关题目
 是满足下列两个条件的无穷数列
是满足下列两个条件的无穷数列 的集合:
的集合: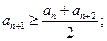 ②
②
 是与
是与 无关的常数.
无关的常数. 是其前n项的和,
是其前n项的和, ,证明:
,证明: ;
; 的通项为
的通项为 ,求
,求 的各项均为正整数,且
的各项均为正整数,且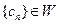 ,试证
,试证 .
.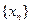 满足
满足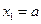 ,
,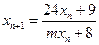
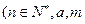 是实数).
是实数).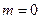 ,
,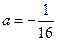 ,求通项
,求通项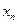 ;
;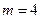 ,设数列
,设数列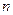 项和当
项和当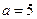 时为
时为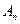 ,当
,当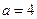 时为
时为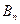 ,
,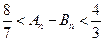
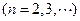 .
. 和
和 中,已知
中,已知 ,其中
,其中 且
且 。
。 ,求数列
,求数列 的前n项和;
的前n项和; 时,数列
时,数列 ,试问在区间[1,a]上是否存在实数b使得
,试问在区间[1,a]上是否存在实数b使得 ,若存在,求出b的一切可能的取值及相应的集合C;若不存在,说明理由。
,若存在,求出b的一切可能的取值及相应的集合C;若不存在,说明理由。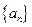 满足:
满足: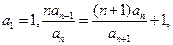 令
令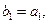
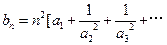
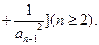
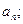
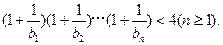
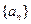 中,
中,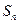 是其前
是其前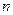 项和,若
项和,若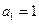 ,
,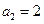 ,
,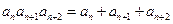 ,
,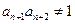 ,则
,则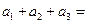 _______________,
_______________,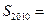 _______________.
_______________.
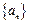 满足
满足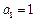 ,
,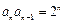 (
(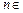 N
N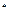 ),则
),则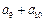 的值为 .
的值为 .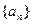 中,
中,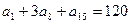 ,则
,则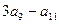 的值为多少?
的值为多少?